
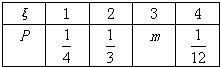 设随机变量ξ的概率分布如表所示:
设随机变量ξ的概率分布如表所示: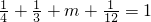 ,
, ,
,

 +
+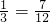
 ,(x≤1)
,(x≤1) ,(1<X≤2)
,(1<X≤2) ,(2<x≤3)
,(2<x≤3)

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:013
设随机变量x的概率分布为p(x=K)=PK·(1-P)1-K(K=0.1)。则Ex、Dx的值分别是( )
A.0和1 B.P和P 2
C.P和1-P D.P和(1-P)P
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
A.0和1 B.P和P 2
C.P和1-P D.P和(1-P)P
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省高三第六次(4月)周测理科数学试卷(解析版) 题型:解答题
在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(1)求随机变量 =5的概率;
=5的概率;
(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2010年宁夏青铜峡市高二下学期期末考试(理科)数学卷 题型:解答题
(本小题满分12分) 设随机变量X的概率分布为 (k=1,2,3,4):
(k=1,2,3,4):
(Ⅰ)确定常数 的值;
的值;
(Ⅱ)写出 的分布列;
的分布列;
(Ⅲ)计算 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com