
【题目】设命题![]() :
: ![]() ,函数
,函数![]() 有意义;命题
有意义;命题![]() :
: ![]() ,不等式
,不等式![]() 恒成立,如果命题“
恒成立,如果命题“![]() 或
或![]() ”为真命题,命题“
”为真命题,命题“![]() 且
且![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】有人说:“掷一枚骰子一次得到的点数是2的概率是![]() ,这说明掷一枚骰子6次会出现一次点数是2.”对此说法,同学中出现了两种不同的看法:一些同学认为这种说法是正确的.他们的理由是:因为掷一枚骰子一次得到点数是2的概率是
,这说明掷一枚骰子6次会出现一次点数是2.”对此说法,同学中出现了两种不同的看法:一些同学认为这种说法是正确的.他们的理由是:因为掷一枚骰子一次得到点数是2的概率是![]() ,所以掷一枚骰子6次得到一次点数是2的概率P=
,所以掷一枚骰子6次得到一次点数是2的概率P=![]() ×6=1,即“掷一枚骰子6次会出现一次点数是2”是必然事件,一定发生.还有一些同学觉得这种说法是错误的,但是他们却讲不出是什么理由来.你认为这种说法对吗?请说出你的理由.
×6=1,即“掷一枚骰子6次会出现一次点数是2”是必然事件,一定发生.还有一些同学觉得这种说法是错误的,但是他们却讲不出是什么理由来.你认为这种说法对吗?请说出你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() 的中点.
的中点.
(Ⅰ)证明: ![]() ;
;
(Ⅱ)若![]() 为
为![]() 上的动点,
上的动点, ![]() 与平面
与平面![]() 所成最大角的正切值为
所成最大角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知经过原点的直线与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆上不同于
为椭圆上不同于![]() 的一点,直线
的一点,直线![]() 的斜率均存在,且直线
的斜率均存在,且直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若![]() ,设
,设![]() 分别为椭圆的左、右焦点,斜率为
分别为椭圆的左、右焦点,斜率为![]() 的直线
的直线![]() 经过椭圆的右焦点,且与椭圆交于
经过椭圆的右焦点,且与椭圆交于![]() 两点,若点
两点,若点![]() 在以
在以![]() 为直径的圆内部,求
为直径的圆内部,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上. (Ⅰ)求证:EF⊥平面PAC;
(Ⅱ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求 ![]() 的值.
的值.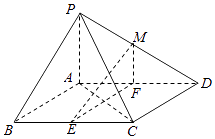
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 恒过点
恒过点![]() ,且与直线
,且与直线![]() :
: ![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)探究在曲线![]() 上,是否存在异于原点的两点
上,是否存在异于原点的两点![]() ,
, ![]() ,当
,当![]() 时,直线
时,直线![]() 恒过定点?若存在,求出该定点坐标;若不存在,请说明理由.
恒过定点?若存在,求出该定点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于被墨水污染,一道数学题仅能见到如下文字:“已知二次函数![]() 的图像经过
的图像经过![]() ,
,![]() ,求证:这个二次函数的图像关于直线
,求证:这个二次函数的图像关于直线![]() 对称”,根据已知消息,题中二次函数图像不具有的性质是( ).
对称”,根据已知消息,题中二次函数图像不具有的性质是( ).
A. 在![]() 轴上的截线段长是
轴上的截线段长是![]() B. 与
B. 与![]() 轴交于点
轴交于点![]()
C. 顶点![]() D. 过点
D. 过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”;若
的“不动点”;若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”.函数
的“稳定点”.函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )设函数
)设函数![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求证:
)求证:![]() .
.
(![]() )设函数
)设函数![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com