
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦点分别为
,焦点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 面积的最大值是
面积的最大值是![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 是坐标原点,若
是坐标原点,若![]() 判定四边形
判定四边形![]() 的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
【答案】(Ⅰ) ![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)由题意得到![]() 的方程组,求出
的方程组,求出![]() 的值,即可得出椭圆方程;
的值,即可得出椭圆方程;
(Ⅱ)当直线![]() 的斜率不存在时,易求出四边形
的斜率不存在时,易求出四边形![]() 的面积;当直线
的面积;当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 方程是
方程是![]() ,联立直线与椭圆方程,结合判别式和韦达定理,可表示出弦长
,联立直线与椭圆方程,结合判别式和韦达定理,可表示出弦长![]() ,再求出点
,再求出点![]() 到直线
到直线![]() 的距离,根据
的距离,根据![]() 和点
和点![]() 在曲线
在曲线![]() 上,求出
上,求出![]() 的关系式,
的关系式,
最后根据![]() ,即可得出结果.
,即可得出结果.
解:(Ⅰ)由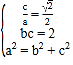 解得
解得![]() 得椭圆
得椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() 或
或![]() ,此时四边形
,此时四边形![]() 的面积为
的面积为![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 方程是
方程是![]() ,联立椭圆方程
,联立椭圆方程
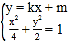
![]()
![]() ,
,![]()
![]()
![]()
点![]() 到直线
到直线![]() 的距离是
的距离是![]()
由![]() 得
得![]()
因为点![]() 在曲线
在曲线![]() 上,所以有
上,所以有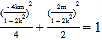 整理得
整理得![]()
由题意四边形![]() 为平行四边形,所以四边形
为平行四边形,所以四边形![]() 的面积为
的面积为
![]()
由![]() 得
得![]() , 故四边形
, 故四边形![]() 的面积是定值,其定值为
的面积是定值,其定值为![]() .
.


科目:高中数学 来源: 题型:
【题目】为征求个人所得税法修改建议,某机构对当地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)).
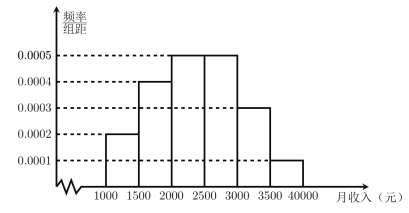
(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图估算样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中用分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-a|+|2x-1|(a∈R).
(1)当a=-1时,求f(x)≤2的解集;
(2)若f(x)≤|2x+1|的解集包含集合![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有5个大小相同的球,其中有2个白球,2个黑球,1个红球,现从袋中每次取出1球,去除后不放回,直到取到有两种不同颜色的球时即终止,用![]() 表示终止取球时所需的取球次数,则随机变量
表示终止取球时所需的取球次数,则随机变量![]() 的数字期望
的数字期望![]() 是( )
是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 两个居民小区的居委会欲组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动.两个校区每位同学的往返车费及服务老人的人数如下表:
两个居民小区的居委会欲组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动.两个校区每位同学的往返车费及服务老人的人数如下表:
|
| |
往返车费 | 3元 | 5元 |
服务老人的人数 | 5人 | 3人 |
根据安排,去敬老院的往返总车费不能超过37元,且![]() 小区参加献爱心活动的同学比
小区参加献爱心活动的同学比![]() 小区的同学至少多1人,则接受服务的老人最多有____人.
小区的同学至少多1人,则接受服务的老人最多有____人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为k的直线l与椭圆M有两个不同的交点A,B.
.斜率为k的直线l与椭圆M有两个不同的交点A,B.
(Ⅰ)求椭圆M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点
,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点![]() 共线,求k.
共线,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是圆x2+y2=4上的动点,P点在x轴上的射影是D,点M满足![]() .
.

(Ⅰ)求动点M的轨迹C的方程
(Ⅱ)设A、B是轨迹C上的不同两点,点E(﹣4,0),且满足![]() ,若λ∈[
,若λ∈[![]() ,1),求直线AB的斜率k的取值范围.
,1),求直线AB的斜率k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com