练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某班共有名学生，已知以下信息：

    ①男生共有人；

    ②女团员共有人；

    ③住校的女生共有人；

    ④不住校的团员共有人；

    ⑤住校的男团员共有人；

    ⑥男生中非团员且不住校的共有人；

    ⑦女生中非团员且不住校的共有人．

    根据以上信息，该班住校生共有______人

    【答案】

    【解析】

    通过分类讨论得出如下表格即可求出答案．

    （1）女生共有人，其中住校的有人，则不住校的有人，

    住校

    不住校

    总共

    女团员

    女非团员

    男团员

    男非团员

    而不住校的非团员共有人，不住校的团员有人，由女团员共有人，住校的女团员人；

    （2）由不住校的团员共有人，而其中女团员人，不住校的男团员有人，又男生中非团员且不住校的共有人；

    综上可知：①不住校的男团员有人，女团员人；②不住校的男非团员人，女非团员人．

    即不住校的学生共有人，因此该班住校生共有人．

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知在图1所示的梯形中，，于点，且.将梯形沿折起，使平面平面，如图2所示，连接，取的中点.

    (1)求证：平面平面；

    (2)设，求几何体的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在棱长为2的正方体中，，分别为棱、的中点，为棱上的一点，且，设点为的中点，则点到平面的距离为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次田径比赛中，35名运动员的成绩（单位：分钟）的茎叶图如图所示。

    若将运动员按成绩由好到差编为1—35号，再用系统抽样方法从中抽取5人，则其中成绩在区间上的运动员人数为

    A.6B.5C.4D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法中：

    ①若，满足，则的最大值为；

    ②若，则函数的最小值为

    ③若，满足，则的最小值为

    ④函数的最小值为

    正确的有__________．（把你认为正确的序号全部写上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，AB//CD，且

    （1）证明：平面PAB⊥平面PAD；

    （2）若PA=PD=AB=DC, ,且四棱锥P-ABCD的体积为，求该四棱锥的侧面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C的顶点为坐标原点O，对称轴为x轴，其准线过点.

    (1)求抛物线C的方程；

    (2)过抛物线焦点F作直线l，使得抛物线C上恰有三个点到直线l的距离都为，求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给定椭圆，称圆心在坐标原点，半径为的圆是椭圆的“伴椭圆”，若椭圆右焦点坐标为，且过点.

    （1）求椭圆的“伴椭圆”方程；

    （2）在椭圆的“伴椭圆”上取一点，过该点作椭圆的两条切线、，证明：两线垂直；

    （3）在双曲线上找一点作椭圆的两条切线，分别交于切点、使得，求满足条件的所有点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

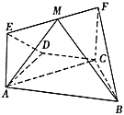
    【题目】如图，在等腰梯形中，，，，四边形为矩形，平面平面，.

    （1）求证：平面；

    （2）点在线段上运动，设平面与平面所成二面角的平面角为（），试求的取值范围.

    查看答案和解析>>

    同步练习册答案