
【题目】执行如图所示的程序框图,若输出s的值为11,那么输入的n值等于( ) 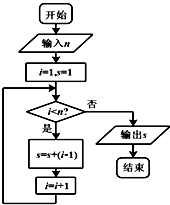
A.5
B.6
C.7
D.8
【答案】B
【解析】解:当i=1,S=1时,不满足输出条件,故进行循环,执行完循环体后,S=1,i=2;
当i=2,S=1时,不满足输出条件,故进行循环,执行完循环体后,S=2,i=3;
当i=3,S=2时,不满足输出条件,故进行循环,执行完循环体后,S=4,i=4;
当i=4,S=4时,不满足输出条件,故进行循环,执行完循环体后,S=7,i=5;
当i=5,S=7时,不满足输出条件,故进行循环,执行完循环体后,S=11,i=6;
当i=6,S=11时,满足输出条件,
故进行循环的条件应为:i<6,
即输入n的值是6,
故选:B.
【考点精析】关于本题考查的程序框图,需要了解程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,M(﹣2,0).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A(ρ,θ)为曲线C上一点,B(ρ,θ+ ![]() ),且|BM|=1.
),且|BM|=1.
(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)求|OA|2+|MA|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() 与两个定点
与两个定点![]() ,
,![]() 的距离之比为
的距离之比为![]() .
.
(1)求点![]() 的坐标所满足的关系式;
的坐标所满足的关系式;
(2)求![]() 面积的最大值;
面积的最大值;
(3)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,各个侧面均是边长为
中,各个侧面均是边长为![]() 的正方形,
的正方形,![]() 为线段
为线段![]() 的中点.
的中点.
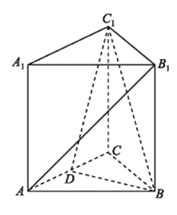
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(3)设![]() 为线段
为线段![]() 上任意一点,在
上任意一点,在![]() 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点![]() ,使
,使![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x|+|x﹣1|.
(Ⅰ)若f(x)≥|m﹣1|恒成立,求实数m的最大值M;
(Ⅱ)在(Ⅰ)成立的条件下,正实数a,b满足a2+b2=M,证明:a+b≥2ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=3cos2x的图象,只需把函数y=3sin(2x+ ![]() )的图象上所有的点( )
)的图象上所有的点( )
A.向右平行移动 ![]() 个单位长度
个单位长度
B.向右平行移动 ![]() 个单位长度
个单位长度
C.向左平行移动 ![]() 个单位长度
个单位长度
D.向左平移移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
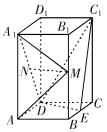
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年04月13日“山东济南非法经营疫苗系列案件”披露后,引发社会高度关注,引起公众、受种者和儿童家长对涉案疫苗安全性和有效性的担忧。为采取后续处置措施提供依据,保障受种者的健康,尽快恢复公众接种疫苗的信心,科学严谨地分析涉案疫苗接种给受种者带来的安全性风险和是否有效,对某疫苗预防疾病的效果,进行动物实验,得到下面表格中的统计数据:现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
未发病 | 发病 | 合计 | |
未注射疫苗 |
|
|
|
注射疫苗 |
|
|
|
合计 |
|
|
|
(1)求![]() 列联表中的数据
列联表中的数据![]() 的值;
的值;
(2)绘制发病率的条形统计图,并判断疫苗是否有效?
|
|
|
|
|
|
|
|
|
|
(3)能够有多大把握认为疫苗有效?
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据相关规定,24小时内的降水量为日降水量(单位:mm),不同的日降水量对应的降水强度如表:
日降水量 | (0,10) | [10,25) | [25,50) | [50,100) | [100,250) | [250,+∞) |
降水强度 | 小雨 | 中雨 | 大雨 | 暴雨 | 大暴雨 | 特大暴雨 |
为分析某市“主汛期”的降水情况,从该市2015年6月~8月有降水记录的监测数据中,随机抽取10天的数据作为样本,具体数据如下:
16 12 23 65 24 37 39 21 36 68
(1)请完成以如表示这组数据的茎叶图; 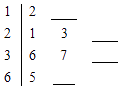
(2)从样本中降水强度为大雨以上(含大雨)天气的5天中随机选取2天,求恰有1天是暴雨天气的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com