
【题目】已知函数![]() ,对于任意的实数
,对于任意的实数![]() ,
,![]() 恒成立.
恒成立.
(1)求![]() 的值;
的值;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据![]() 和
和![]() ,可知
,可知![]() ,也为极小值,可得必要条件
,也为极小值,可得必要条件![]() ,求得
,求得![]() ;接着证明充分性,当
;接着证明充分性,当![]() 时,利用导数可得函数单调性,从而知充分性成立,由此得到结果;
时,利用导数可得函数单调性,从而知充分性成立,由此得到结果;
(2)设![]() ,整理得到
,整理得到![]() ,构造函数
,构造函数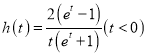 ,利用导数可证得
,利用导数可证得![]() ,从而说明
,从而说明![]() ,得到
,得到![]() ,解不等式即可得到所证结论.
,解不等式即可得到所证结论.
(1)由题意得:![]() .
.
![]() 且
且![]() 恒成立,
恒成立,![]() 是
是![]() 的最小值,也是
的最小值,也是![]() 的极小值,
的极小值,
则其必要条件![]() ,则
,则![]() ,解得:
,解得:![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,可知充分性成立;
,可知充分性成立;
综上所述:![]() .
.
(2)由(1)可知:![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() 不妨设
不妨设![]() ,
,![]() ,
,
![]()
![]() ,
,
 ,令
,令![]() ,则
,则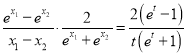 ,
,
令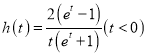 ,
,
则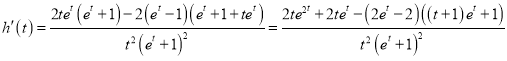
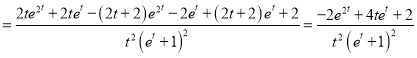 ,
,
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
, ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() ,
,
即![]() ,解得:
,解得:![]() 或
或![]() (舍),
(舍),
综上所述:![]() .
.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】随着网购人数的日益增多,网上的支付方式也呈现一种多样化的状态,越来越多的便捷移动支付方式受到了人们的青睐,更被网友们评为“新四大发明”之一.随着人们消费观念的进步,许多人喜欢用信用卡购物,考虑到这一点,一种“网上的信用卡”横空出世——蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式,简单便捷,同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系,某网站对其注册用户开展抽样调查,在每个年龄段的注册用户中各随机抽取100人,得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如图所示.
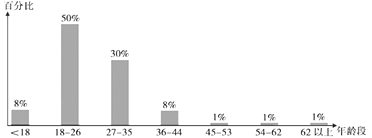
(1)由大数据可知,在18到44岁之间使用花呗“赊购”的人数百分比y与年龄x成线性相关关系,利用统计图表中的数据,以各年龄段的区间中点代表该年龄段的年龄,求所调查群体各年龄段“赊购”人数百分比y与年龄x的线性回归方程(回归直线方程的斜率和截距保留两位有效数字);
(2)该网站年龄为20岁的注册用户共有2000人,试估算该网站20岁的注册用户中使用花呗“赊购”的人数;
(3)已知该网店中年龄段在18-26岁和27-35岁的注册用户人数相同,现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人,再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度,求抽取的两人年龄都在18到26岁的概率.
参考答案: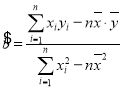 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() :ρ(2cosθ-sinθ)=6.
:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的![]() 、2倍后得到曲线C2,试写出直线
、2倍后得到曲线C2,试写出直线![]() 的直角坐标方程和曲线C2的参数方程.
的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)当m=1时,求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的一个顶点与抛物线
的一个顶点与抛物线![]() 的焦点重合,
的焦点重合,![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,离心率
的左、右焦点,离心率![]() ,过椭圆
,过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在直线![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
(Ⅲ)设点![]() 是一个动点,若直线
是一个动点,若直线![]() 的斜率存在,且
的斜率存在,且![]() 为
为![]() 中点,
中点,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据《环境空气质量指数![]() 技术规定(试行)》规定:空气质量指数在区间
技术规定(试行)》规定:空气质量指数在区间![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 时,其对应的空气质量状况分别为优、良、轻度污染、中度污染、重度污染、严重污染.如图为某市2019年10月1日至10月7日的空气质量指数
时,其对应的空气质量状况分别为优、良、轻度污染、中度污染、重度污染、严重污染.如图为某市2019年10月1日至10月7日的空气质量指数![]() 直方图,在这7天内,下列结论正确的是( )
直方图,在这7天内,下列结论正确的是( )
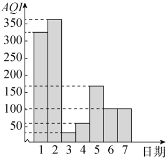
A.前4天![]() 的方差小于后3天
的方差小于后3天![]() 的方差
的方差
B.这7天内空气质量状况为严重污染的天数为3
C.这7天的平均空气质量状况为良
D.空气质量状况为优或良的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为折痕把
为折痕把![]() 折起,当几何体
折起,当几何体![]() 的的体积最大时,则下列命题中正确的个数是( )
的的体积最大时,则下列命题中正确的个数是( )

①![]()
②![]() ∥平面
∥平面![]()
③![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角
所成的角
④![]() 与
与![]() 所成的角等于
所成的角等于![]() 与
与![]() 所成的角
所成的角
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|x+1|+|x-2|.
(1)求f(x)的最小值m;
(2)若a,b,c均为正实数,且满足a+b+c=m,求证:![]() +
+![]() +
+![]() ≥3.
≥3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com