
【题目】如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1 , M,N分别是A1B,B1C1的中点.
(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成的角的大小.
【答案】
(1)证明:如图,由已知BC⊥AC,BC⊥CC1,得BC⊥平面ACC1A1.连接AC1,则BC⊥AC1.
又侧面ACC1A1是正方形,所以A1C⊥AC1.
又BC∩A1C=C,所以AC1⊥平面A1BC.
因为侧面ABB1A1是正方形,M是A1B的中点,连接AB1,则点M是AB1的中点.
又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1.故MN⊥平面A1BC.
(2)解:如图所示,因为AC1⊥平面A1BC,设AC1与A1C相交于点D,
连接BD,则∠C1BD为直线BC1和平面A1BC所成的角.
设AC=BC=CC1=a,则C1D= ![]() a,BC1=
a,BC1= ![]() a.
a.
在Rt△BDC1中,sin ∠C1BD= ![]() =
= ![]() ,所以∠C1BD=30°,故直线BC1和平面A1BC所成的角为30°.
,所以∠C1BD=30°,故直线BC1和平面A1BC所成的角为30°.
【解析】(I)证明线面垂直,关键是证明线线垂直,根据BC⊥AC1,A1C⊥AC1,AC1⊥平面A1BC,又因为MN∥AC1,可得;
(II)由AC1⊥平面A1BC,得∠C1BD为直线BC1和平面A1BC所成的角,解三角形![]() 即可.
即可.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD= ![]() ,AB=AC.
,AB=AC. 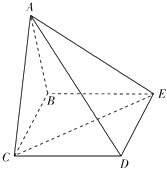
(1)证明:AD⊥CE;
(2)设CE与平面ABE所成的角为45°,求二面角C﹣AD﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年“五一节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题: 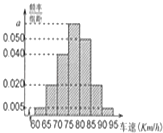
(1)求a的值,并说明交警部门采用的是什么抽样方法?
(2)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(3)若该路段的车速达到或超过90km/h即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= ![]() )
)
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点P是双曲线 ![]() ﹣y2=1的右支上一点,M、N分别是(x+
﹣y2=1的右支上一点,M、N分别是(x+ ![]() )2+y2=1和(x﹣
)2+y2=1和(x﹣ ![]() )2+y2=1上的点,则|PM|﹣|PN|的最大值是( )
)2+y2=1上的点,则|PM|﹣|PN|的最大值是( )
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=1,当n≥2时,Sn=2an .
(1)求证数列{an}为等比数列,并求出an的通项公式;
(2)设若bn=an+1﹣1,设数列{anbn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2﹣x+ ![]() a)的定义域为R;命题q:不等式
a)的定义域为R;命题q:不等式 ![]() <1+ax对一切正实数均成立.如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围.
<1+ax对一切正实数均成立.如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com