
某人要制作一个三角形,要求它的三条高的长度分别是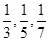 ,则此人 ( )
,则此人 ( )
A.不能作出这样的三角形 B.能作出一个锐角三角形
C.能作出一个直角三角形 D.能作出一个钝角三角形
D
【解析】
试题分析:分别设出三条高对应的三角形边长,设三角形的面积为k,根据等积法即可用k表示出a,b及c,然后利用余弦定理表示出cosC,把表示出的a,b及c代入即可求出cosC的值,根据cosC的值小于0和C的范围,即可得到C为钝角,从而得到三角形为钝角三角形.。解:设此三角形的三边长分别为a,b及c,则即a=6k,b=10k,c=14k,根据余弦定理得:cosC=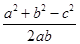 <0,∵C∈(0,π),∴C为钝角,则此人能作出一个钝角三角形.故选D
<0,∵C∈(0,π),∴C为钝角,则此人能作出一个钝角三角形.故选D
考点:余弦定理
点评:此题考查了余弦定理,设出三角形的三边,利用等积法表示出三角形三边是本题的突破点,熟练掌握余弦定理是解本题的关键.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
| 1 |
| 13 |
| 1 |
| 11 |
| 1 |
| 5 |
| A、不能作出这样的三角形 |
| B、作出一个锐角三角形 |
| C、作出一个直角三角形 |
| D、作出一个钝角三角形 |
查看答案和解析>>
科目:高中数学 来源:2014届山东省聊城市高二第四次模块检测文科数学卷(解析版) 题型:选择题
某人要制作一个三角形,要求它的三条高的长度分别为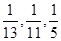 ,则此人能( )
,则此人能( )
A.不能作出这样的三角形 B.作出一个锐角三角形
C.作出一个直角三角形 D.作出一个钝角三角形
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省四地六校高一下学期第一次月考数学试卷 题型:选择题
某人要制作一个三角形,要求它的三条高的长度分别为 ,则此人( )
,则此人( )
A.不能作出这样的三角形 B.能作出一个锐角三角形
C.能作出一个直角三角形 D.能作出一个钝角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com