
【题目】在无穷数列![]() 中,
中,![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,
,![]() ,设
,设![]() ,记使得
,记使得![]() 成立的
成立的![]() 的最大值为
的最大值为![]() .
.
(![]() )设数列
)设数列![]() 为
为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,写出
,写出![]() ,
,![]() ,
,![]() 的值.
的值.
(![]() )若
)若![]() 为等比数列,且
为等比数列,且![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,直线
中,直线 ![]() 的参数方程为
的参数方程为 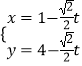 (
( ![]() 为参数).再以原点为极点,以
为参数).再以原点为极点,以 ![]() 正半轴为极轴建立极坐标系,并使得它与直角坐标系
正半轴为极轴建立极坐标系,并使得它与直角坐标系 ![]() 有相同的长度单位.在该极坐标系中圆
有相同的长度单位.在该极坐标系中圆 ![]() 的方程为
的方程为 ![]() .
.
(1)求圆 ![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆 ![]() 与直线
与直线 ![]() 交于点
交于点 ![]() 、
、 ![]() ,若点
,若点 ![]() 的坐标为
的坐标为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地早潮叫潮,晚潮叫汐,在通常的情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋。下面是某港口某季节一天的时间与水深的关系表:
时刻( | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
水深/米( | 5 | 7.6 | 5.0 | 2.4 | 5.0 | 7.6 | 5.0 | 2.4 | 5.0 |
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,并分别求出10:00时和13:00时的水深近似数值。
(2)若某船的吃水深度(船底与水面的距离)为4.5米,安全条例规定至少要有1.8米的安全间隙(船底与洋底的距离),该船何时能进入港口,在港口能呆多久?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.

(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A1,A2,A3;田忌的三匹马分别为B1,B2,B3;三匹马各比赛一次,胜两场者获胜,双方均不知对方的马出场顺序.
(1)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>A3>B3,则田忌获胜的概率是多大?
(2)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>B3>A3,则田忌获胜的概率是多大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原面积为![]() .计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
.计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】猎人在相距100 m处射击一野兔,命中的概率为![]() ,若第一次未击中,则猎人进行第二次射击,但距离已是150 m,若又未击中,则猎人进行第三次射击,但距离已是200 m,已知此猎人命中的概率与距离的平方成反比,求射击不超过三次击中野兔的概率.
,若第一次未击中,则猎人进行第二次射击,但距离已是150 m,若又未击中,则猎人进行第三次射击,但距离已是200 m,已知此猎人命中的概率与距离的平方成反比,求射击不超过三次击中野兔的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1: ![]() ,(t为参数)曲线C2:
,(t为参数)曲线C2: ![]() +y2=4.
+y2=4.
(1)在同一平面直角坐标系中,将曲线C2上的点按坐标变换y′=yx,后得到曲线C′.求曲线C′的普通方程,并写出它的参数方程;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C′上的动点,求PQ中点M到直线C3:
,Q为C′上的动点,求PQ中点M到直线C3: ![]() (t为参数)的距离的最小值.
(t为参数)的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com