练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】100辆汽车通过某一段公路时，时速的频率分布直方图如图所示，则时速在[50，70）的汽车大约有（　　）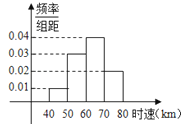

    A.60辆
    B.80辆
    C.70辆
    D.140辆

    【答案】C
    【解析】解：由直方图可知，时速在[50，60]的频率为0.03×10=0.3 时速在[60，70]的频率为0.04×10=0.4
    所以时速在[50，70]的汽车大约有100×（0.3+0.4）=70辆，
    故选：C．
    【考点精析】根据题目的已知条件，利用用样本的频率分布估计总体分布的相关知识可以得到问题的答案，需要掌握样本数据的频率分布表和频率分布直方图，是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律，它可以让我们更清楚的看到整个样本数据的频率分布情况，并由此估计总体的分布情况．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】【2017广东佛山二模】设函数，其中，是自然对数的底数.

    （Ⅰ）若是上的增函数，求的取值范围；

    （Ⅱ）若，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方体ABCD﹣A1B1C1D1中，动点P在底面ABCD内，且P到棱AD的距离与到面对角线BC1的距离相等，则点P的轨迹是（　　）
    A.线段
    B.椭圆的一部分
    C.双曲线的一部分
    D.抛物线的一部分

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2017辽宁葫芦岛市二模】已知数列满足： .

    （1）求数列的通项公式；

    （2）若,求数列的前项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前项和为Sn ， 且Sn= ，{bn}为等差数列，且a1=b1 ， a2（b2﹣b1）=a1 ．
    （1）求数列{an}和{bn}通项公式；
    （2）设 ，求数列{cn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果执行如图所示的框图，输入N=5，则输出的数等于（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A、B、C所对的边分别是a、b、c，且满足csinA﹣ acosC=0．
    （1）求角C的大小；
    （2）若c=2，求△ABC的面积S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中，AC⊥BC，AB⊥BB1 ， AC=BC=BB1 ， D为AB的中点，且CD⊥DA1 ．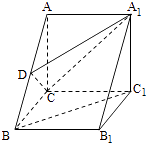

    （1）求证：BC1∥平面DCA1；
    （2）求BC1与平面ABB1A1所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a，b∈R，且ab≠0，则下列结论恒成立的是（ ）
    A.a+b≥2
    B.a2+b2＞2ab
    C.+ ≥2
    D.| + |≥2

    查看答案和解析>>

    同步练习册答案