
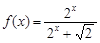 的图象上两点P1(x1,y1)、P2(x2,y2),若
的图象上两点P1(x1,y1)、P2(x2,y2),若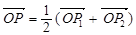 ,且点P的横坐标为
,且点P的横坐标为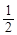 .
.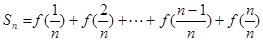
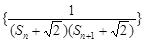 的前n项和,若
的前n项和,若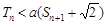 对一切n∈N*都成立,试求a的取值范围。
对一切n∈N*都成立,试求a的取值范围。 ;(3)
;(3) .
.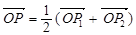 ,那么利用坐标化简得到结论。
,那么利用坐标化简得到结论。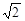 ,结合倒序相加法求解得到结论。
,结合倒序相加法求解得到结论。 ,裂项求和的数学思想得到证明。
,裂项求和的数学思想得到证明。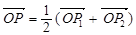 ,∴P是P1P2的的中点Þx1+x2=1------(2分)
,∴P是P1P2的的中点Þx1+x2=1------(2分)

 .-----------------------------(4分)
.-----------------------------(4分)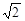 ,
,  ,
,

 (n-1个1)
(n-1个1)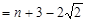 ∴
∴ .------------(8分)
.------------(8分)
 --------------------(10分)
--------------------(10分) 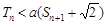 Û
Û  ∵
∵ ≥8,当且仅当n=4时,取“=” ∴
≥8,当且仅当n=4时,取“=” ∴ ,因此,
,因此, -------------------(12分)
-------------------(12分)

科目:高中数学 来源:不详 题型:单选题
 ,直线
,直线 :
: ,
, 为平面上的动点,过点
为平面上的动点,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,且
,且 ,动点
,动点 的轨迹为
的轨迹为 ,已知圆
,已知圆 过定点
过定点 ,圆心
,圆心 在轨迹
在轨迹 上运动,且圆
上运动,且圆 与
与 轴交于
轴交于 、
、 两点,设
两点,设 ,
, ,则
,则 的最大值为
的最大值为 A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com