
【题目】如图,点P在正方体ABCD﹣A1B1C1D1的表面上运动,且P到直线BC与直线C1D1的距离相等,如果将正方体在平面内展开,那么动点P的轨迹在展开图中的形状是( ) 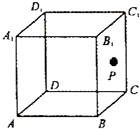
A.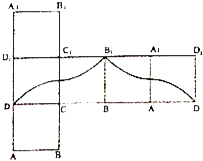
B.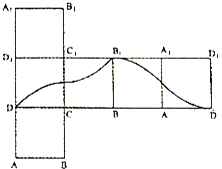
C.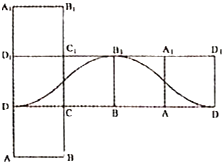
D.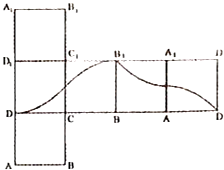
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x2)+ax.(a≤0)
(1)若f(x)在x=0处取得极值,求a的值;
(2)讨论f(x)的单调性;
(3)证明:(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<
)< ![]() (n∈N* , e为自然对数的底数).
(n∈N* , e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xoy中,直线l的参数方程是 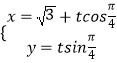 (t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是
(t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是 ![]() +ρ2sin2θ=1.
+ρ2sin2θ=1.
(1)求曲线C的直角坐标方程;
(2)求直线l与曲线C相交所得的弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点坐标为![]() ,且短轴一顶点
,且短轴一顶点![]() 满足
满足![]() .
.
(1)求椭圆的方程;
(2)过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图,则函数表达式为;若将该函数向左平移1个单位,再保持纵坐标不变,横坐标缩短为原来的 ![]() 倍得到函数g(x)= .
倍得到函数g(x)= . 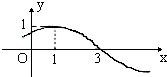
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四面体ABCD的顶点C在平面α内,且直线BC与平面α所成角为15°,顶点B在平面α上的射影为点O,当顶点A与点O的距离最大时,直线CD与平面α所成角的正弦值为 . 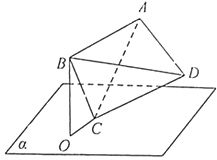
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com