
【题目】某电视台举办青年歌手大奖赛,有十名评委打分,已知甲、乙两名选手演唱后的得分如茎叶图如图所示.
(1)从统计学的角度,你认为甲与乙比较,演唱水平怎样?
(2)现场有三名点评嘉宾A,B,C,每位选手可以从中选两位接受其指导,若选手选每位点评嘉宾的可能性相等,求甲、乙两名选手选择的点评嘉宾恰有一人重复的概率.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3mx+n(m>0)的极大值为6,极小值为2.
(1)求实数m,n的值;
(2)求f(x)在区间[0,3]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点. 
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面APD⊥平面ABCD,且PA=PD=AD=2,在线段PC上是否存在点M,使二面角M﹣BQ﹣C的大小为60°.若存在,试确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其
范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的部分直方图如图所示.
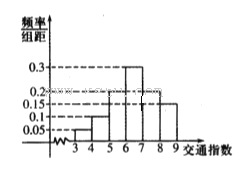
(1)请补全直方图,并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个?
(2)用分层抽样的方法从交通指数在[4,6),[6,8),[8,l0]的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽出的6个路段中任取2个,求至少一个路段为轻度拥堵的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取某校一个年级的部分学生进行一分钟跳绳次数的测试,将数据整理后,画出频率分布直方图如图所示.已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.
(1)求第四小组的频率;
(2)求参加这次测试的学生的人数;
(3)若一分钟跳绳次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asinA=4bsinB,ac= ![]() (a2﹣b2﹣c2).(13分)
(a2﹣b2﹣c2).(13分)
(Ⅰ)求cosA的值;
(Ⅱ)求sin(2B﹣A)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com