
| 父亲身高(x) | 60 | 62 | 64 | 65 | 66 | 67 | 68 | 70 | 72 | 74 |
| 儿子身高(y) | 63.6 | 65.2 | 66 | 65.5 | 66.9 | 67.1 | 67.4 | 68.3 | 70.1 | 70 |
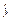 ="0.464" 6x+35.974 7(3)当父亲身高为73英寸时,估计儿子的身高约为69.9英寸。
="0.464" 6x+35.974 7(3)当父亲身高为73英寸时,估计儿子的身高约为69.9英寸。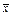 =66.8,
=66.8,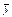 =67.01,
=67.01,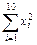 ="44" 794,
="44" 794,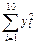 ="44" 941.93,
="44" 941.93,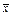
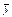 ="4" 476.268,
="4" 476.268,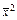 ="4" 462.24,
="4" 462.24,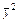 ≈4 490.34,
≈4 490.34, 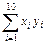 ="44" 842.4.
="44" 842.4.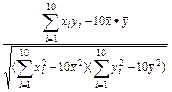
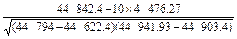
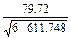 ≈0.980 4.
≈0.980 4.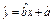 .
.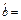
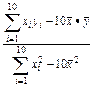 =
=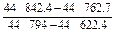
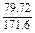 ≈0.464 6.
≈0.464 6.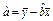 ="67.01-0.464" 6×66.8≈35.974 7.
="67.01-0.464" 6×66.8≈35.974 7.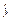 ="0.464" 6x+35.974 7.
="0.464" 6x+35.974 7.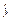 ="0.464" 6×73+35.974 7≈69.9,
="0.464" 6×73+35.974 7≈69.9,

 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:不详 题型:解答题
| 数据 | 1 | 2 | 3 | … | n |
| 变量x | x1 | x2 | x3 | … | xn |
| 变量y | y1 | y2 | y3 | … | yn |
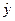 =bx+a;将y为自变量,x为因变量,得回归方程为
=bx+a;将y为自变量,x为因变量,得回归方程为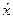 =b′y+a′.
=b′y+a′.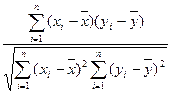 ,它可表示两个变量线性关系的强弱.
,它可表示两个变量线性关系的强弱.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 家庭编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xi(收入)千元 | 0.8 | 1.1 | 1.3 | 1.5 | 1.5 | 1.8 | 2.0 | 2.2 | 2.4 | 2.8 |
| yi(支出)千元 | 0.7 | 1.0 | 1.2 | 1.0 | 1.3 | 1.5 | 1.3 | 1.7 | 2.0 | 2.5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.甲种水稻比乙种水稻分蘖整齐 |
| B.乙种水稻比甲种水稻分蘖整齐 |
| C.甲、乙两种水稻分蘖整齐程度相同 |
| D.甲、乙两种水稻分蘖整齐程度不能比较 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
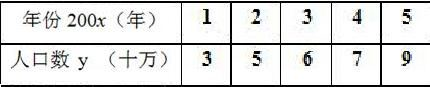
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.相关系数用来衡量变量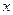 与 与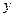 之间的线性相关程度 之间的线性相关程度 |
B.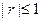 ,且 ,且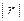 越接近于1,相关程度越大 越接近于1,相关程度越大 |
C.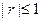 ,且 ,且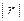 越接近于0,相关程度越小 越接近于0,相关程度越小 |
D.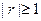 ,且 ,且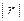 越接近于1,相关程度越大 越接近于1,相关程度越大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com