练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    过点（-2，3）的抛物线的标准方程为
     
    ．
    分析：根据点（-2，3），设抛物线方程为x2=2py，或y2=-2px（p＞0），再代入点的坐标，即可得出结论．
    解答：解：由题意，设抛物线方程为x2=2py，或y2=-2px（p＞0），则
    将点（-2，3）代入可得4=6p或9=4p，
    ∴p=
    2
    3
    或p=
    9
    4
    ．
    ∴所求抛物线的标准方程为x2=
    4
    3
    y，或y2=-
    9
    2
    x．
    故答案为：x2=
    4
    3
    y，或y2=-
    9
    2
    x．
    点评：本题考查抛物线的标准方程，考查学生的计算能力，确定抛物线的类型是关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网已知点D（0，-2），过点D作抛线C1：x2=2py（p＞0）的切线l，切点A在第一象限，如图．
    （1）求切点A的纵坐标；
    （2）若离心率为
    		3
    2
    的椭圆C：
    y2
    a 2
    +
    x2
    b2
    =1（a＞b＞0）恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k2，k3，若2k1+k2=3k，求抛物线C1和椭圆C2的方程．
    （3）设P、Q分别是（2）中的椭圆C2的右顶点和上顶点，M是椭圆C2在第一象限的任意一点，求四边形OPMQ面积的最大值以及此时M点的坐标．

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：044

    在平面直线坐标系，xOy中，直线l与抛线y2＝2x相交于A、B两点．

    (1)求证：如果直线l过点(3，0)，那么·＝3”是真命题．

    (2)写出(1)中命题的逆命题，判断它是真命题还是假命题，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：山东省实验中学2011届高三5月针对性练习数学理综试题 题型：044

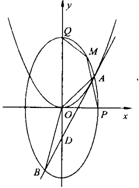
    已知点D(0，－2)，过点D作抛线C1：x2＝2py(p＞0)的切线l，切点A在第一象限，如图．

    (1)求切点A的纵坐标；

    (2)若离心率为的椭圆恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k1，k2，若2k1＋k2＝3k，求抛物线C1和椭圆C2的方程．

    (3)设P、Q分别是(2)中的椭圆C2的右顶点和上顶点，M是椭圆C2在第一象限的任意一点，求四边形OPMQ面积的最大值以及此时M点的坐标．

    查看答案和解析>>

    同步练习册答案