练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某地西红柿2月1日开始上市，通过市场调查，得到西红柿的种植成本Q（单位：元/100kg）与上市时间（单位：天）的数据如下表：
    时间
    		50
    		110
    		250
    种植成本Q
    		150
    		108
    		150
       根据表中数据，下列函数模型中可以描述西红柿的种植成本Q与上市时间的变化关系的是            （   ）
    A．B．
    C．D．
    B
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

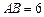    设，在线段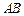上任取两点C,D（端点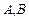除外），将线段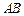分成三条线段AC,CD,DB.
    （1）若分成的三条线段的长度均为正整数，求这三条线段可以构成三角形（称事件A）的概率；
    （2）若分成的三条线段的长度均为正实数，求这三条线段可以构成三角形（称事件B）的概率；
    （3）根据以下用计算机所产生的20组随机数，试用随机数摸拟的方法，来近似计算（Ⅱ）中事件B的概率.
    20组随机数如下：
     
    		1组
    		2组
    		3组
    		4组
    		5组
    		6组
    		7组
    		8组
    		9组
    		10组
    X
    		0.52
    		0.36
    		0.58
    		0.73
    		0.41
    		0.6
    		0.05
    		0.32
    		0.38
    		0.73
    Y
    		0.76
    		0.39
    		0.37
    		0.01
    		0.04
    		0.28
    		0.03
    		0.15
    		0.14
    		0.86
     
     
    		11组
    		12组
    		13组
    		14组
    		15组
    		16组
    		17组
    		18组
    		19组
    		20组
    X
    		0.67
    		0.47
    		0.58
    		0.21
    		0.54
    		0.64
    		0.36
    		0.35
    		0.95
    		0.14
    Y
    		0.41
    		0.54
    		0.51
    		0.37
    		0.31
    		0.23
    		0.56
    		0.89
    		0.17
    		0.03
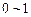    （X是之间的均匀随机数，Y也是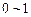之间的均匀随机数）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本题满分12分)
    某校举行的数学知识竞赛中，将参赛学生的成绩在进行整理后分成5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组．已知第三小组的频数是15．
    (1)求成绩在50—70分的频率是多少；
    (2)求这次参赛学生的总人数是多少；
    (3)求这次数学竞赛成绩的平均分的近似值．

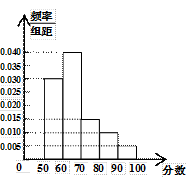
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）高三年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：
    分组
    		频数
    		频率

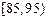    		①
    		②

    		 
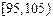    		0.050

    		 
    		0.200

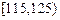    		12
    		0.300

    		 
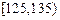    		0.275

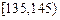    		4
    		③

    		 
    		0.050
    合 计
    		 
    		④
    （1）根据上面图表，①、②、③、④处的数值分别是多少？
    （2）在坐标系中画出的频率分布直方图；
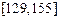    （3）根据题中信息估计总体平均数，并估计总体落在中的概率。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本题满分12分)
    网络对现代人的生活影响较大, 尤其对青少年. 为了了解网络对中学生学习成绩的影响, 某地区教育局从辖区高中生中随机抽取了1000人进行调查, 具体数据如下列联表所示．
     
    		经常上网
    		不经常上网
    		合计
    不及格
    		80
    		a
    		200
    及格
    		b
    		680
    		c
    合计
    		200
    		d
    		1000
    (1)求a,b,c,d；
    (2)利用独立性检验判断, 有多大把握认为上网对高中生的学习成绩有关．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分分）某学校高三年级有学生1000名，经调查研究,其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼(称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学.
    (Ⅰ)求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
    (Ⅱ) 测得该年级所抽查的100名同学身高(单位：厘米) 频率分布直方图如右图：
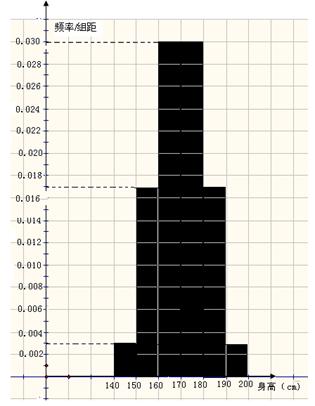
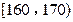    (ⅰ) 统计方法中，同一组数据常用该组区间的中点值（例如区间的中点值为165）作为代表．据此，计算这100名学生身高数据的期望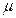及标准差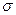(精确到0.1)；
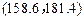    (ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在范围中的学生的人数．
    (Ⅲ) 如果以身高达170cm作为达标的标准，对抽取的100名学生,得到下列联表:
    体育锻炼与身高达标2×2列联表
     
    		身高达标
    		身高不达标
    		总计
    积极参加体育锻炼
    		40
    		 
    		 
    不积极参加体育锻炼
    		 
    		15
    		 
    总计
    		 
    		 
    		100
    (ⅰ)完成上表；
    (ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
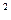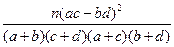    参考公式:K=,参考数据:
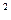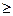    P(Kk)
    		0.40
    		0.25
    		0.15
    		0.10
    		0.05
    		0.025
    k
    		0.708
    		1.323
    		2.072
    		2.706
    		3.841
    		5.024

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    在调查的480名男人中有38名患有色盲，520名女人中有6名患有色盲，分别利用图形和独立性检验的方法来判断色盲与性别是否有关？你所得到的结论在什么范围内有效？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在对分类变量X, Y进行独立性检验时,算得=7有以下四种判断
    (p(K2>6.635)="0.010" )
    (1) 有99﹪的把握认为X与Y有关;(2)有99﹪的把握认为X与Y无关;(3)在假设H0:X与Y 无关的前提下有99﹪的把握认为X与Y有关;(4)在假设H1: X与Y有关的前提下有99﹪的把握认为X与Y无关.以上4个判断正确的是 （    ）
    A．(1)、(2) B．(1)、(3)C．(2)、(4)D．(3)、(4)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    独立性检验中，假设：变量X与变量Y没有关系．则在成立的情况下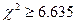，表示的意义是（   ）
    A．变量X与变量Y有关系的概率为1%
    B．变量X与变量Y有关系的概率为99%
    变量X与变量Y没有关系的概率为99%
    D．变量X与变量Y没有关系的概率为99.9%

    查看答案和解析>>

    同步练习册答案