已知数列{an},{bn},满足条件an+1=2an+k(k≠0),bn=an+1-an≠0.
(1)求证:数列{bn}是等比数列;
(2)若k=a1=1,求数列{an},{bn}的通项公式.
(1)证明:∵a
n+1=2a
n+k(k≠0),
∴a
n=2a
n-1+k
∴a
n+1-a
n=2(a
n-a
n-1)
∵b
n=a
n+1-a
n≠0.
∴b
n=2b
n-1∴数列{b
n}是以2为公比的等比数列
(2)解:∵k=a
1=1,
∴a
2=2a
1+1=3
∴b
1=a
2-a
1=2
由(1)可得数列{b
n}是以2为公比,以2为首项的等比数列
∴
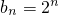
即

∴a
2-a
1=2
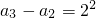
…

以上n-1个式子相加可得,a
n-a
1=2+2
2+2
3+…+2
n-1=
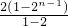
=2
n-2
∴
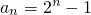
分析:(1)由∵a
n+1=2a
n+k(k≠0),可得a
n=2a
n-1+k,两式相减可得a
n+1-a
n=2(a
n-a
n-1),可证
(2)由(1)及已知可求b
n,结合已知b
n=a
n+1-a
n≠0可得

,利用叠加可求a
n点评:本题主要考查了利用数列的递推公式构造等比数列,等比数列的通项公式的应用,叠加法的应用在数列的通项公式中的应用

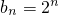

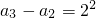

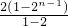 =2n-2
=2n-2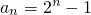
 ,利用叠加可求an
,利用叠加可求an

 阅读快车系列答案
阅读快车系列答案