
【题目】已知四棱柱![]() 的底面是边长为
的底面是边长为![]() 的菱形,且
的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
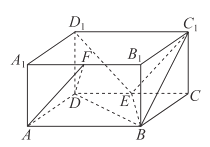
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 和平面
和平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 中点为
中点为![]() ,求证四边形
,求证四边形![]() 为平行四边形,即可由线线平行推证线面平行;
为平行四边形,即可由线线平行推证线面平行;
(2)以![]() 为坐标原点,建立空间直角坐标系,通过求解两平面法向量之间夹角的余弦值,从而求得二面角夹角的余弦值.
为坐标原点,建立空间直角坐标系,通过求解两平面法向量之间夹角的余弦值,从而求得二面角夹角的余弦值.
(1)证明:∵![]() ,
,![]() ,∴
,∴![]() 是
是![]() 中点,
中点,
取![]() 中点
中点![]() ,连
,连![]() ,
,![]() ,如下图所示:
,如下图所示:
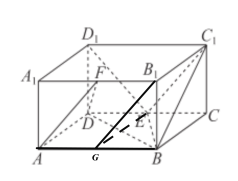
则在菱形![]() 中,
中,![]() ,
,![]() //
//![]()
∵![]() ,
,![]() //
//![]() ,∴
,∴![]() ,
,![]() //
//![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() //
//![]() ,
,
又![]() ,
,![]() //
//![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() //
//![]() ,∴
,∴![]() //
//![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() //平面
//平面![]() .即证.
.即证.
(2)以![]() 为原点,以
为原点,以![]() 分别为
分别为![]() 建立如图所示的空间的直角坐标系.
建立如图所示的空间的直角坐标系.
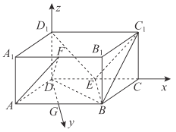
因为已知该四棱柱为直四棱柱,![]() ,
,![]() ,
,
所以![]() 为等边三角形.
为等边三角形.
因为![]() ,所以点
,所以点![]() 是
是![]() 的中点.
的中点.
故点![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.
由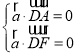 得
得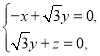
取![]() ,得
,得![]() ,
,![]() ,
,
故![]()
![]() .
.
∵![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
∴![]() ,∴
,∴![]() 是平面
是平面![]() 的法向量,
的法向量,
设平面![]() 和平面
和平面![]() 所成锐角为
所成锐角为![]() ,
,
则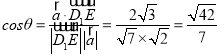 .
.
即平面![]() 和平面
和平面![]() 所成锐角的余弦值为
所成锐角的余弦值为![]() .
.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(e+x)=f(e﹣x),且f(0)=0,当x∈(0,e]时,f(x)=lnx已知方程![]() 在区间[﹣e,3e]上所有的实数根之和为3ea,将函数
在区间[﹣e,3e]上所有的实数根之和为3ea,将函数![]() 的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
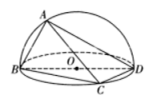
【题目】如图,已知![]() 是圆
是圆![]() 的直径,
的直径,![]() ,
,![]() 在圆上且分别在
在圆上且分别在![]() 的两侧,其中
的两侧,其中![]() ,
,![]() .现将其沿
.现将其沿![]() 折起使得二面角
折起使得二面角![]() 为直二面角,则下列说法不正确的是( )
为直二面角,则下列说法不正确的是( )
A.![]() ,
,![]() ,
,![]() ,
,![]() 在同一个球面上
在同一个球面上
B.当![]() 时,三棱锥
时,三棱锥![]() 的体积为
的体积为![]()
C.![]() 与
与![]() 是异面直线且不垂直
是异面直线且不垂直
D.存在一个位置,使得平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高考的成绩不仅需要平时的积累,还与考试时的状态有关系.为了了解考前学生的紧张程度与性别是否有关系,现随机抽取某校500名学生进行了调查,结果如表所示:
心情 性别 | 男 | 女 | 总计 |
正常 | 30 | 40 | 70 |
焦虑 | 270 | 160 | 430 |
总计 | 300 | 200 | 500 |
(1)根据该校调查数据,能否在犯错误的概率不超过0.01的前提下,认为“该学校学生的考前焦虑情况与性别有关”?
(2)若从考前心情正常的学生中按性别用分层抽样的方法抽取7人,再从被抽取的7人中随机抽取2人,求这两人中有女生的概率.
附: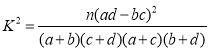 ,
,![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P是△PMN的顶点,M(﹣2,0),N(2,0),直线PM,PN的斜率之积为﹣![]() .
.
(1)求点P的轨迹E的方程;
(2)设四边形ABCD的顶点都在曲线E上,且AB∥CD,直线AB,CD分别过点(﹣1,0),(1,0),求四边形ABCD的面积为![]() 时,直线AB的方程.
时,直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 对任意实数
对任意实数![]() ,
,![]() 满足:
满足:![]() ,且
,且![]() ,
,![]() ,并且当
,并且当![]() 时,
时,![]() .给出如下结论:①函数
.给出如下结论:①函数![]() 是偶函数;②函数
是偶函数;②函数![]() 在
在![]() 上单调递增;③函数
上单调递增;③函数![]() 是以2为周期的周期函数;④
是以2为周期的周期函数;④![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com