
【题目】设函数f(x)=|x﹣a|,a∈R. (Ⅰ)当a=2时,解不等式:f(x)≥6﹣|2x﹣5|;
(Ⅱ)若关于x的不等式f(x)≤4的解集为[﹣1,7],且两正数s和t满足2s+t=a,求证: ![]() .
.
【答案】解:(Ⅰ)当a=2时,不等式:f(x)≥6﹣|2x﹣5|,可化为|x﹣2|+|2x﹣5|≥6. ① x≥2.5时,不等式可化为x﹣2+2x﹣5≥6,∴x≥ ![]() ;
;
②2≤x<2.5,不等式可化为x﹣2+5﹣2x≥6,∴x∈;
③x<2,不等式可化为2﹣x+5﹣2x≥6,∴x≤ ![]() ,
,
综上所述,不等式的解集为(﹣ ![]() ]
] ![]() ;
;
(Ⅱ)证明:不等式f(x)≤4的解集为[a﹣4,a+4]=[﹣1,7],∴a=3,
∴ ![]() =
= ![]() (
( ![]() )(2s+t)=
)(2s+t)= ![]() (10+
(10+ ![]() +
+ ![]() )≥6,当且仅当s=
)≥6,当且仅当s= ![]() ,t=2时取等号
,t=2时取等号
【解析】(Ⅰ)利用绝对值的意义表示成分段函数形式,解不等式即可.(2)根据不等式的解集求出a=3,利用1的代换结合基本不等式进行证明即可.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y= ![]() (x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
(x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( ) 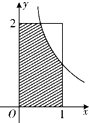
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x)满足f(x﹣4)=﹣f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[﹣8,8]上有四个不同的根x1 , x2 , x3 , x4 , 则x1+x2+x3+x4= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() 的左焦点为F1 , 右焦点为F2 , 过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
的左焦点为F1 , 右焦点为F2 , 过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形. 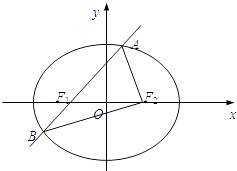
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:①以PQ为直径的圆与x轴的位置关系? ②在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中,P为底面正方形ABCD内一个动点,Q为棱AA1上的一个动点,若|PQ|=2,则PQ的中点M的轨迹所形成图形的面积是( )
A.![]()
B.![]()
C.3
D.4π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一组数据如表:
x | 1 | 2 | 3 | 4 | 5 |
y | 1.3 | 1.9 | 2.5 | 2.7 | 3.6 |
(1)画出散点图;
(2)根据下面提供的参考公式,求出回归直线方程,并估计当x=8时,y的值.
(参考公式: ![]() =
=  =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为F1、F2 , 且两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2 , 则e1e2+1的取值范围为( )
A.(1,+∞)
B.( ![]() ,+∞)
,+∞)
C.( ![]() ,+∞)
,+∞)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨,硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨,硝酸盐15吨.现库存磷酸盐10吨,硝酸盐66吨,在此基础上生产这两种混合肥料.如果生产1车皮甲种肥料产生的利润为12 000元,生产1车皮乙种肥料产生的利润为7 000元,那么可产生的最大利润是( )
A.29 000元
B.31 000元
C.38 000元
D.45 000元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com