
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据第2题求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
【答案】
(1)解:把所给的四对数据写成对应的点的坐标,
在坐标系中描出来,得到散点图如下;
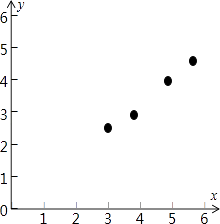
(2)解:由对照数据,计算得
![]() =
= ![]() ×(3+4+5+6)=4.5,
×(3+4+5+6)=4.5,
![]() =
= ![]() ×(2.5+3+4+4.5)=3.5,
×(2.5+3+4+4.5)=3.5,
![]() =32+42+52+62=86,
=32+42+52+62=86,
![]() xiyi=3×2.5+4×3+5×4+6×4.5=66.5,
xiyi=3×2.5+4×3+5×4+6×4.5=66.5,
∴回归方程的系数为 ![]() =
= ![]() =0.7,
=0.7,
![]() =3.5﹣0.7×4.5=0.35,
=3.5﹣0.7×4.5=0.35,
∴所求线性回归方程为 ![]() =0.7x+0.35
=0.7x+0.35
(3)解:由(2)的线性回归方程,估计生产100吨甲产品的生产能耗为
0.7×100+0.35=70.35(吨),
∴90﹣70.35=19.65吨,
预测比技改前降低了19.65吨标准煤
【解析】(1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图;(2)根据所给的这组数据求出回归方程的系数,得到线性回归方程;(3)根据线性回归方程,计算x=100时的生产能耗,求出比技改前降低的标准煤.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2﹣alnx(a∈R)
x2﹣alnx(a∈R)
(1)若函数f(x)在x=2处的切线方程为y=x+b,求a,b的值;
(2)讨论方程f(x)=0解的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,4]上的最大值为9,最小值为1,记f(x)=g(|x|)。
(1)求实数a,b的值;
(2)若不等式f(2k)>1成立,求实数k的取值范围;
(3)定义在[p,q]上的函数![]() (x),设p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式
(x),设p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() (x)为在[p,q]上的有界变差函数。试判断函数f(x)是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由。
(x)为在[p,q]上的有界变差函数。试判断函数f(x)是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如表 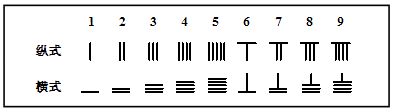
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推,例如6613用算筹表示就是: ![]() ,则9117用算筹可表示为( )
,则9117用算筹可表示为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy 中,已知圆C的参数方程为 ![]() (φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(1)求圆的极坐标方程;
(2)直线l的极坐方程是 ![]() ,射线OM:θ=
,射线OM:θ= ![]() 与圆的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与圆的交点为O,P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元.某月甲、乙两户共交水费y元,已知甲、乙两用户该月用水量分别为5x,3x吨. (Ⅰ) 若x=1,求该月甲、乙两户的水费;
(Ⅱ) 求y关于x的函数;
(Ⅲ) 若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱ABCA1B1C1中,AB=2,AA1=3,
D为C1B的中点,P为AB边上的动点.
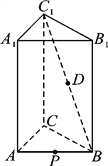
(1)当点P为AB的中点时,证明DP∥平面ACC1A1;
(2)若AP=3PB,求三棱锥BCDP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在二项式( ![]() +
+ ![]() )n展开式中,前三项的系数成等差数列. 求:(1)展开式中各项系数和;
)n展开式中,前三项的系数成等差数列. 求:(1)展开式中各项系数和;
【答案】解:由题意得2 ![]() ×
× ![]() =1+
=1+ ![]() ×
× ![]() ,
,
化为:n2﹣9n+8=0,解得n=1(舍去)或8.
∴n=8.
在 ![]() 中,令x=1,可得展开式中各项系数和=
中,令x=1,可得展开式中各项系数和= ![]() =
= ![]() .
.
(1)展开式中系数最大的项.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com