
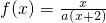 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,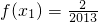 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*)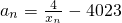 且
且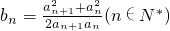 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.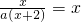 ,可化简为ax(x+2)=x∴ax2+(2a-1)x=0
,可化简为ax(x+2)=x∴ax2+(2a-1)x=0 时,方程x=f(x)有唯一解.
时,方程x=f(x)有唯一解.
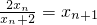
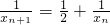 ,即
,即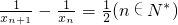
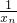 是以
是以 为首项,
为首项, 为公差的等差数列.
为公差的等差数列.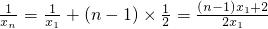 ,∴
,∴
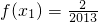 ,
,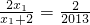 ,即
,即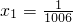
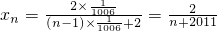
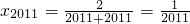
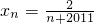 ,
,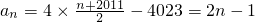 ∴
∴
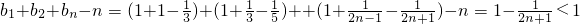
 ,由此能求出f(x)的表达式;
,由此能求出f(x)的表达式;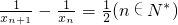 ,由 等差数列的定义可求出数列{xn}的通项公式;
,由 等差数列的定义可求出数列{xn}的通项公式;


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:广东省期末题 题型:解答题
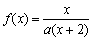 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数, ,f(xn)=xn+1(n∈N*)。 (1)求f(x)的表达式;
,f(xn)=xn+1(n∈N*)。 (1)求f(x)的表达式;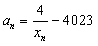 且
且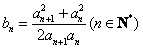 ,求证:
,求证: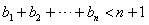 。
。 查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省实验中学、华师附中、广雅中学、深圳中学四校联考高三(上)期末数学试卷(文科)(解析版) 题型:解答题
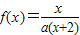 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,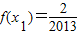 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*)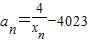 且
且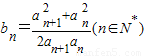 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.查看答案和解析>>
科目:高中数学 来源:2011年江西省抚州市临川二中高考数学一模试卷(文科)(解析版) 题型:解答题
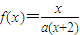 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,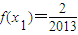 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*)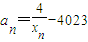 且
且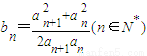 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市东城区东直门中学高三数学提高测试试卷6(文科)(解析版) 题型:解答题
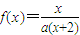 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,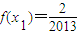 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*) 且
且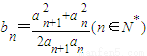 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com