
【题目】已知曲线C的极坐标方程ρ=2cosθ,直线l的参数方程是 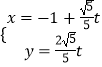 (t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设直线l与y轴的交点是M,N是曲线C上一动点,求|MN|的最大值.
【答案】解:(Ⅰ)曲线C的极坐标方程可化为ρ2=2ρcosθ, 又x2+y2=ρ2 , x=ρcosθ,
∴曲线C的直角坐标方程为x2+y2﹣2x=0.
(Ⅱ)将直线l的参数方程化为直角坐标方程,得y=2x+2,
令x=0得y=2,即M点的坐标为(0,2).
又曲线C为圆,圆C的圆心坐标为(1,0),半径r=1,
则|MC|= ![]() ,
,
|MN|≤|MC|+r= ![]() +1.
+1.
∴MN的最大值为 ![]() +1
+1
【解析】(Ⅰ)曲线C的极坐标方程可化为ρ2=2ρcosθ,利用x2+y2=ρ2 , x=ρcosθ,即可得出;(Ⅱ)求出点M与圆心的距离d,即可得出最小值.
【考点精析】通过灵活运用函数的最值及其几何意义,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 C: ![]() =1( a>b>0)经过点 (1,
=1( a>b>0)经过点 (1, ![]() ),离心率为
),离心率为 ![]() ,点 A 为椭圆 C 的右顶点,直线 l 与椭圆相交于不同于点 A 的两个点P (x1 , y1),Q (x2 , y2).
,点 A 为椭圆 C 的右顶点,直线 l 与椭圆相交于不同于点 A 的两个点P (x1 , y1),Q (x2 , y2).
(Ⅰ)求椭圆 C 的标准方程;
(Ⅱ)当 ![]()
![]() =0 时,求△OPQ 面积的最大值;
=0 时,求△OPQ 面积的最大值;
(Ⅲ)若直线 l 的斜率为 2,求证:△APQ 的外接圆恒过一个异于点 A 的定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技博览会展出的智能机器人有 A,B,C,D 四种型号,每种型号至少有 4 台.要求每 位购买者只能购买1台某种型号的机器人,且购买其中任意一种型号的机器人是等可能的.现在有 4 个人要购买机器人.
(Ⅰ)在会场展览台上,展出方已放好了 A,B,C,D 四种型号的机器人各一台,现把他们 排成一排表演节目,求 A 型与 B 型相邻且 C 型与 D 型不相邻的概率;
(Ⅱ)设这 4 个人购买的机器人的型号种数为ξ,求ξ 的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱ABC﹣A1B1C1中,△ABC为等边三角形,AA1⊥平面ABC,AA1=AB,M,N分别是A1B1 , A1C1的中点,则BM与AN所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(m+2cos2x)cos(2x+θ)为奇函数,且f( ![]() )=0,其中m∈R,θ∈(0,π)
)=0,其中m∈R,θ∈(0,π)
(Ⅰ)求函数f(x)的图象的对称中心和单调递增区间
(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,且f( ![]() +
+ ![]() )=﹣
)=﹣ ![]() ,c=1,ab=2
,c=1,ab=2 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,手机已经成为人们日常生活中不可缺少的产品,手机的功能也日趋完善,已延伸到了各个领域,如拍照,聊天,阅读,缴费,购物,理财,娱乐,办公等等,手机的价格差距也很大,为分析人们购买手机的消费情况,现对某小区随机抽取了200人进行手机价格的调查,统计如下:
年龄 价格 | 5000元及以上 | 3000元﹣4999元 | 1000元﹣2999元 | 1000元以下 |
45岁及以下 | 12 | 28 | 66 | 4 |
45岁以上 | 3 | 17 | 46 | 24 |
(Ⅰ)完成关于人们使用手机的价格和年龄的2×2列联表,再判断能否在犯错误的概率不超过0.025的前提下,认为人们使用手机的价格和年龄有关?
(Ⅱ)从样本中手机价格在5000元及以上的人群中选择3人调查其收入状况,设3人中年龄在45岁及以下的人数为随机变量X,求随机变量X的分布列及数学期望.
附K2= ![]()
P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加数学文化知识竞赛培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下: 甲:8281797895889384
乙:9295807583809085
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加正式比赛,从所抽取的两组数据分析,你认为选派哪位同学参加较为合适?并说明理由;
(Ⅲ)若对甲同学在今后的3次测试成绩进行预测,记这3次成绩中高于80分的次数为ξ(将甲8次成绩中高于80分的频率视为概率),求ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 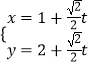 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ. (Ⅰ)求直角坐标下圆C的标准方程;
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ. (Ⅰ)求直角坐标下圆C的标准方程;
(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com