
【题目】| ![]() |=1,|
|=1,| ![]() |=
|= ![]() ,
, ![]()
![]() =0,点C在∠AOB内,且∠AOC=30°,设
=0,点C在∠AOB内,且∠AOC=30°,设 ![]() =m
=m ![]() +n
+n ![]() (m、n∈R),则
(m、n∈R),则 ![]() 等于( )
等于( )
A.![]()
B.3
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】已知三棱锥A﹣BCD的各个棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( ) 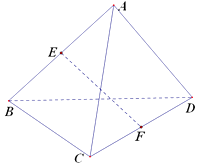
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() :
: ![]() ,过点
,过点![]() 的一条直线与抛物线
的一条直线与抛物线![]() 交于
交于![]() 两点,若抛物线在
两点,若抛物线在![]() 两点的切线交于点
两点的切线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 的斜率存在,取为
的斜率存在,取为![]() ,取直线
,取直线![]() 的斜率为
的斜率为![]() ,请验证
,请验证![]() 是否为定值?若是,计算出该值;若不是,请说明理由.
是否为定值?若是,计算出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆x2+4y2=4,直线l:y=x+m
(1)若l与椭圆有一个公共点,求m的值;
(2)若l与椭圆相交于P、Q两点,且|PQ|等于椭圆的短轴长,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组: ![]() 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。

(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C所对边的长分别为a、b、c,则下列命题:
①若ab>c2 , 则C ![]() ;
;
②若a+b>2c,则C ![]() ;
;
③若a3+b3=c3 , 则C ![]() ;
;
④若(a+b)c<2ab,则ab>c2;
⑤若(a2+b2)c2<2a2b2 , 则C ![]() .
.
其中正确命题是(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}与{bn},若a1=3且对任意正整数n满足an+1﹣an=2,数列{bn}的前n项和Sn=n2+an .
(1)求数列{an},{bn}的通项公式;
(2)求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]() ,且
,且![]() 的最小值为
的最小值为![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,其中
恒成立,其中![]() 是自然对数的底数,求
是自然对数的底数,求![]() 的取值范围;
的取值范围;
(3)设曲线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,且两曲线在点
,且两曲线在点![]() 处的切线分别为
处的切线分别为![]() ,
, ![]() .试判断
.试判断![]() ,
, ![]() 与
与![]() 轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】证明与化简.
(1)求证:cotα=tanα+2cot2α;
(2)请利用(1)的结论证明:cotα=tanα+2tan2α+4cot4α;
(3)请你把(2)的结论推到更一般的情形,使之成为推广后的特例,并加以证明:
(4)化简:tan5°+2tan10°+4tan20°+8tan50°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com