
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 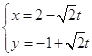 (
( ![]() 为参数),以原点
为参数),以原点 ![]() 为极点,以
为极点,以 ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)求曲线 ![]() 的普通方程与曲线
的普通方程与曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)试判断曲线 ![]() 与
与 ![]() 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察研究某种植物的生长速度与温度的关系,经过统计,得到生长速度(单位:毫米/月)与月平均气温的对比表如下:
温度 | -5 | 0 | 6 | 8 | 12 | 15 | 20 |
生长速度 | 2 | 4 | 5 | 6 | 7 | 8 | 10 |
(1)求生长速度![]() 关于温度
关于温度![]() 的线性回归方程;(斜率和截距均保留为三位有效数字);
的线性回归方程;(斜率和截距均保留为三位有效数字);
(2)利用(1)中的线性回归方程,分析气温从![]() 至
至![]() 时生长速度的变化情况,如果某月的平均气温是
时生长速度的变化情况,如果某月的平均气温是![]() 时,预测这月大约能生长多少.
时,预测这月大约能生长多少.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
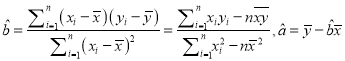 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC上的点,AD=AE,F是BC的中点,AF与DE交于点G,△ABF沿AF折起,得到如图2所示的三棱锥A﹣BCF,其中BC= ![]() .
. 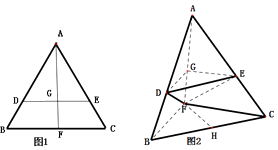
(1)求证:平面DEG∥平面BCF;
(2)若D,E为AB,AC上的中点,H为BC中点,求异面直线AB与FH所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,函数
,函数![]() ,函数
,函数![]() 在
在![]() 轴上的截距我
轴上的截距我![]() ,与
,与![]() 轴最近的最高点的坐标是
轴最近的最高点的坐标是![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)将函数![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位,再将图象上各点的纵坐标不变,横坐标伸长到原来的2倍,得到函数
)个单位,再将图象上各点的纵坐标不变,横坐标伸长到原来的2倍,得到函数![]() 的图象,求
的图象,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥P﹣ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点. 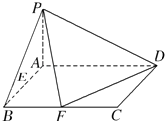
(Ⅰ)证明:PF⊥FD;
(Ⅱ)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(Ⅲ)若PB与平面ABCD所成的角为45°,求二面角A﹣PD﹣F的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com