
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,顺次连接椭圆
,顺次连接椭圆![]() 的四个顶点得到的四边形的面积为16.
的四个顶点得到的四边形的面积为16.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过椭圆![]() 的顶点
的顶点![]() 的直线
的直线![]() 交椭圆于另一点
交椭圆于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 、
、![]() 、
、![]() 成等比数列,求直线
成等比数列,求直线![]() 的斜率.
的斜率.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】根据国家环保部最新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米。某城市环保部分随机抽取的一居民区过去20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
组别 | PM2.5平均浓度 | 频数 | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(II)求样本平均数,并根据样本估计总计的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下图中,四边形 ABCD是等腰梯形, ![]() ,
, ![]() ,O、Q分别为线段AB、CD的中点,OQ与EF的交点为P,OP=1,PQ=2,现将梯形ABCD沿EF折起,使得
,O、Q分别为线段AB、CD的中点,OQ与EF的交点为P,OP=1,PQ=2,现将梯形ABCD沿EF折起,使得![]() ,连结AD、BC,得一几何体如图所示.
,连结AD、BC,得一几何体如图所示.
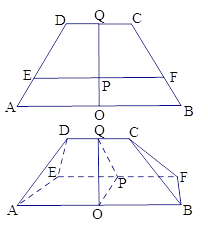
(Ⅰ)证明:平面ABCD![]() 平面ABFE;
平面ABFE;
(Ⅱ)若上图中, ![]() ,CD=2,求平面ADE与平面BCF所成锐二面角的余弦值.
,CD=2,求平面ADE与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
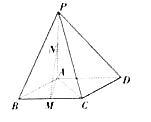
【题目】如图:在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点,且
的中点,且![]() .
.
(1)证明: ![]() 面
面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ;若存在,求出
;若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市两所高中分别组织部分学生参加了“七五普法网络知识大赛”,现从这两所学校的参赛学生中分别随机抽取30名学生的成绩(百分制)作为样本,得到样本数据的茎叶图如图所示.
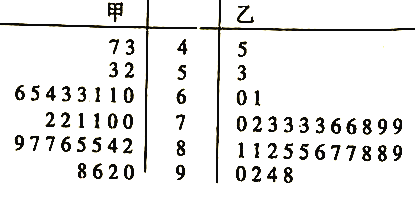
(Ⅰ)若乙校每位学生被抽取的概率为0.15,求乙校参赛学生总人数;
(Ⅱ)根据茎叶图,从平均水平与波动情况两个方面分析甲、乙两校参赛学生成绩(不要求计算);
(Ⅲ)从样本成绩低于60分的学生中随机抽取3人,求3人不在同一学校的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,
为参数,![]() ),其中
),其中![]() ,在以
,在以![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() ,曲线
,曲线![]() .
.
(Ⅰ)求![]() 与
与![]() 交点的直角坐标系;
交点的直角坐标系;
(Ⅱ)若![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com