
【题目】如图①,在等腰梯形![]() 中,
中,![]() 分别为
分别为![]() 的中点
的中点![]()
![]() 为
为![]() 中点,现将四边形
中点,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体,在图②中.
,得到如图②所示的多面体,在图②中. 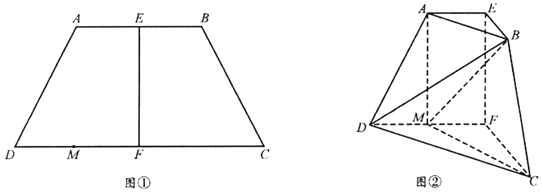
(1)证明:![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】为选拔A,B两名选手参加某项比赛,在选拔测试期间,他们参加选拔的5次测试成绩(满分100分)记录如下:
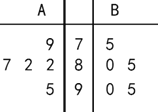
(1)从A,B两人的成绩中各随机抽取一个,求B的成绩比A低的概率;
(2)从统计学的角度考虑,你认为选派哪位选手参加比赛更合适?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查高二年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高(单位:![]() )在
)在![]() 内的男生人数有16人.
内的男生人数有16人.
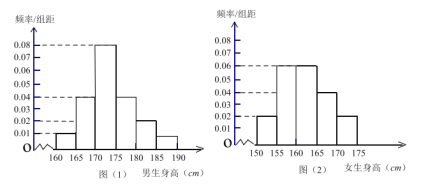
(Ⅰ)求在抽取的学生中,男女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生人数 | |||
女生人数 | |||
总计 |
附:参考公式和临界值表:
 ,
,
| 5.024 | 6.635 | 7.879 | 10.828 |
| 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( ).
A.“![]() ,
,![]() 互为共轭复数”是“
互为共轭复数”是“![]() ”的充分不必要条件
”的充分不必要条件
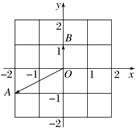
B.如图,在复平面内,若复数![]() ,
,![]() 对应的向量分别是
对应的向量分别是![]() ,
,![]() ,则复数
,则复数![]() 对应的点的坐标为
对应的点的坐标为![]()
C.若函数![]() 恰在
恰在![]() 上单调递减,则实数
上单调递减,则实数![]() 的值为4
的值为4
D.函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到9的九个数字中取三个偶数四个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)上述七位数中三个偶数排在一起的有几个?
(3)在(1)中的七位数中,偶数排在一起、奇数也排在一起的有几个?
(4)在(1)中任意两偶数都不相邻的七位数有几个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() 的左、右焦点分别为F1,F2,离心率为
的左、右焦点分别为F1,F2,离心率为![]() ,点A在椭圆E上,∠F1AF2=60°,△F1AF2的面积为4
,点A在椭圆E上,∠F1AF2=60°,△F1AF2的面积为4![]() .
.
(1)求椭圆E的方程;
(2)过原点O的两条互相垂直的射线与椭圆E分别交于P,Q两点,证明:点O到直线PQ的距离为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为1,若对任意的n∈N*,数列{an}满足an+1﹣3an<2,则称数列{an}具有性质L.
(Ⅰ)判断下面两个数列是否具有性质L:
①1,3,5,7,9,…;
②1,4,16,64,256,…;
(Ⅱ)若{an}是等差数列且具有性质L,其前n项和Sn满足Sn<2n2+2n(n∈N*),求数列{an}的公差d的取值范围;
(Ⅲ)若{an}是公比为正整数的等比数列且具有性质L,设bn=an![]() (n∈N*),且数列{bn}不具有性质L,求数列{an}的通项公式.
(n∈N*),且数列{bn}不具有性质L,求数列{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com