
【题目】已知直线![]() 过点
过点![]() ,且与
,且与![]() 轴、
轴、![]() 轴都交于正半轴,当直线
轴都交于正半轴,当直线![]() 与坐标轴围成的三角形面积取得最小值时,求:
与坐标轴围成的三角形面积取得最小值时,求:
(1)直线![]() 的方程;
的方程;
(2)直线l关于直线m:y=2x-1对称的直线方程.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,点D是A1B的中点,点E是B1C1的中点.
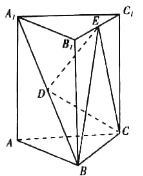
(1)求证:DE∥平面ACC1A1;
(2)若△ABC的面积为![]() ,三棱柱ABC﹣A1B1C1的高为3,求三棱锥D﹣BCE的体积.
,三棱柱ABC﹣A1B1C1的高为3,求三棱锥D﹣BCE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
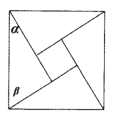
【题目】《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为![]() ,
,![]() ,且小正方形与大正方形面积之比为
,且小正方形与大正方形面积之比为![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 关于直线
关于直线![]() 对称且过点
对称且过点![]() 和
和![]() ,直线
,直线![]() 的方程为:
的方程为:![]() .
.
(1)证明:直线![]() 与圆
与圆![]() 相交;
相交;
(2)记直线![]() 与圆
与圆![]() 的两个交点为
的两个交点为![]() ,
,![]() .
.
①若弦长![]() ,求实数
,求实数![]() 的值;
的值;
②求![]() 面积的最大值及
面积的最大值及![]() 面积的最大时
面积的最大时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解儿子身高与其父亲身高的关系,随机调查了5对父子的身高,统计数据如下表所示.
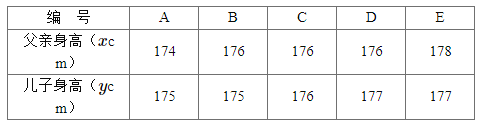
(1)从这五对父子任意选取两对,用编号表示出所有可能取得的结果,并求随机事件M![]() “两对父子中儿子的身高都不低于父亲的身高”发生的概率;
“两对父子中儿子的身高都不低于父亲的身高”发生的概率;
(2)由表中数据,利用“最小二乘法”求![]() 关于
关于![]() 的回归直线的方程.
的回归直线的方程.
参考公式: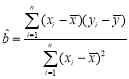 ,
,![]() ;回归直线:
;回归直线:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数
有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数![]() 的取值范围是( )
的取值范围是( )
A. (![]() ,
,![]() ] B. (
] B. (![]() ,
,![]() ] C. [
] C. [![]() ,
,![]() ) D. [
) D. [![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com