
【题目】已知a为实常数,函数f(x)=ex﹣ax﹣1(e为自然对数的底数).
(1)讨论函数f(x)的单调性;
(2)若a≤1,函数f(x)有两个零点,求实数a的取值范围.
【答案】
(1)解:f′(x)=ex﹣a,
当a≤0时,f′(x)>0,函数f(x)在R递增,
当a>0时,f′(x)=ex﹣a,
令f′(x)>0,解得:x>lna,令f′(x)<0,解得:x<lna,
故f(x)在(lna,+∞)递增,在(﹣∞,lna)递减,
综上,a≤0时,函数f(x)在R递增,
a>0时,f(x)在(lna,+∞)递增,在(﹣∞,lna)递减
(2)解:由(1)得,a≤0时,函数f(x)在R递增,不可能有2个零点,
当0<a≤1时,函数f(x)在(﹣∞,lna)递减,在(lna,+∞)递增,
故f(lna)为函数f(x)的最小值,
令k(a)=f(lna)=a﹣alna﹣1,a>0,
k′(a)=1﹣lna﹣1=﹣lna,
令k′(x)>0,解得:0<a<1,
故函数k(a)在(0,1)递增,且k(1)=0,
故a∈(0,1)时,f(lna)<0,
令m(a)=lna﹣(﹣ ![]() )=lna+
)=lna+ ![]() ,a∈(0,1),
,a∈(0,1),
m′(a)= ![]() <0,
<0,
∴m(a)在(0,1)递减,
∴m(a)>m(1)>0,
即a∈(0,1)时,﹣ ![]() <lna<0,
<lna<0,
由于f(﹣ ![]() )=
)= ![]() >0,f(0)=0,
>0,f(0)=0,
当a∈(0,1)时,函数f(x)有2个零点
【解析】(1)利用导函数讨论原函数的增减性。(2)根据导数研究函数在指定区间上的最值,进而得到函数在具体区间上的增减性,故可证明当a∈(0,1)时,函数f(x)有2个零点。
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的最大(小)值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
【题目】某班抽取20名学生周测物理考试成绩(单位:分)的频率分布直方图如下:
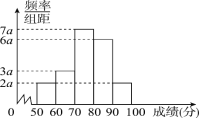
(1)求频率分布直方图中a的值,并写出众数;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生中任选2人,求这2人的成绩都在[60,70)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,其中a∈R. (Ⅰ)给出a的一个取值,使得曲线y=f(x)存在斜率为0的切线,并说明理由;
,其中a∈R. (Ⅰ)给出a的一个取值,使得曲线y=f(x)存在斜率为0的切线,并说明理由;
(Ⅱ)若f(x)存在极小值和极大值,证明:f(x)的极小值大于极大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且 ![]() .
.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an , 求数列 ![]() 的前n项和Tn .
的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的单调递减函数,f′(x)是其导函数,若 ![]() >x,则下列不等关系成立的是( )
>x,则下列不等关系成立的是( )
A.f(2)<2f(1)
B.3f(2)>2f(3)
C.ef(e)<f(e2)
D.ef(e2)>f(e3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论,其中不正确的是( )
①f( ![]() )=
)= ![]()
②函数f(x)在( ![]() ,π)上为减函数
,π)上为减函数
③任意x∈[0, ![]() ],都有f(x)+f(π﹣x)=4.
],都有f(x)+f(π﹣x)=4.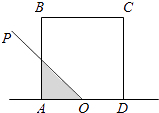
A.①
B.③
C.②
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x+m(m∈R)的图象与x轴相交于A(x1 , 0),B(x2 , 0)两点,且x1<x2 .
(I)若函数f(x)的最大值为2,求m的值;
(Ⅱ)若 ![]() 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(Ⅲ)证明:x1x2<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn(n∈N*),满足Sn=2an﹣1.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com