
【题目】(2015·山东)设函数![]() =
=![]() . 已知曲线
. 已知曲线![]() = 在点
= 在点![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(1)求![]() 的值;
的值;
(2)是否存在自然数![]() ,使得方程
,使得方程![]() =
=![]() 在
在![]() 内存在唯一的根?如果存在,求出k;如果不存在,请说明理由;
内存在唯一的根?如果存在,求出k;如果不存在,请说明理由;
(3)设函数![]() =
=![]()
![]() (
(![]() 表示,
表示,![]() 中的较小值),求
中的较小值),求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)已知函数f(x)=x3+ax+![]() , g(x)=-lnx.
, g(x)=-lnx.
(1)当a为何值时,x轴为曲线y=f(x)的切线;
(2)用min{m,n} 表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(x>0),,讨论h(x)零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)在直角坐标系xOy中,直线l的参数方程为 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,![]() c的极坐标方程为
c的极坐标方程为![]() =2
=2![]() sin
sin![]() .
.
(1)写出![]() c的直角坐标方程;
c的直角坐标方程;
(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)设数列{an}的前n项和为Sn , 已知a1=1, a2=2,且an+1=3Sn-Sn+1+3(n![]() )
)
(1)证明:an+2=3an;
(2)求Sn
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)过点(0,
(a>b>0)过点(0,![]() ),且离心率为
),且离心率为![]() 。
。
(Ⅰ)求椭圆E的方程;
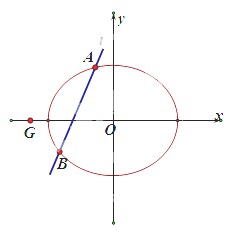
(II)设直线x my 1,(m R)交椭圆E与A,B两点,判断点G(-![]() ,0)与以线段AB为直径的圆的位置关系,并说明理由。
,0)与以线段AB为直径的圆的位置关系,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同,从中任意选取3个。
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)某厂用鲜牛奶在某台设备上生产![]() 两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产
两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产![]() 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
(Ⅰ)求Z的分布列和均值;该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.
(Ⅱ) 若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,下列命题:①
,下列命题:①![]() 时,
时,![]() 为奇函数;②
为奇函数;②![]() 的图象关于
的图象关于![]() 中心对称;③
中心对称;③![]() ,
,![]() 时,方程
时,方程![]() 只有一个实根;④方程
只有一个实根;④方程![]() 至多有两个实根,其中正确的个数有
至多有两个实根,其中正确的个数有![]()
![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上海自贸区某种进口产品的关税税率为![]() ,其市场价格
,其市场价格![]() (单位:千元,
(单位:千元,![]() 与市场供应量
与市场供应量![]() (单位:万件)之间近似满足关系式:
(单位:万件)之间近似满足关系式:![]() .
.
(1)请将![]() 表示为关于
表示为关于![]() 的函数,并根据下列条件计算:若市场价格为7千元,则市场供应量约为2万件.试确定
的函数,并根据下列条件计算:若市场价格为7千元,则市场供应量约为2万件.试确定![]() 的值;
的值;
(2)当![]() 时,经调查,市场需求量
时,经调查,市场需求量![]() (单位:万件)与市场价格
(单位:万件)与市场价格![]() 近似满足关系式:
近似满足关系式:![]() .为保证市场供应量不低于市场需求量,试求市场价格
.为保证市场供应量不低于市场需求量,试求市场价格![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com