
【题目】黄金分割起源于公元前![]() 世纪古希腊的毕达哥拉斯学派,公元前
世纪古希腊的毕达哥拉斯学派,公元前![]() 世纪,古希腊数学家欧多克索斯第一个系统研究了这一问题,公元前
世纪,古希腊数学家欧多克索斯第一个系统研究了这一问题,公元前![]() 年前后欧几里得撰写《几何原本》时吸收了欧多克索斯的研究成果,进一步系统论述了黄金分割,成为最早的有关黄金分割的论著.黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值为
年前后欧几里得撰写《几何原本》时吸收了欧多克索斯的研究成果,进一步系统论述了黄金分割,成为最早的有关黄金分割的论著.黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值为![]() ,把
,把![]() 称为黄金分割数. 已知双曲线
称为黄金分割数. 已知双曲线![]() 的实轴长与焦距的比值恰好是黄金分割数,则
的实轴长与焦距的比值恰好是黄金分割数,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知点M(﹣1,0),N(1,0),曲线E上任意一点到点M的距离均是到点N的距离的![]() 倍.
倍.
(1)求曲线E的方程;
(2)已知m≠0,设直线![]() :x﹣my﹣1=0交曲线E于A,C两点,直线
:x﹣my﹣1=0交曲线E于A,C两点,直线![]() :mx+y﹣m=0交曲线E于B,D两点,若CD的斜率为﹣1时,求直线CD的方程.
:mx+y﹣m=0交曲线E于B,D两点,若CD的斜率为﹣1时,求直线CD的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
:![]() ,
,![]() :
:![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A. 把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数![]() 与仰卧起坐
与仰卧起坐
个数![]() 之间的关系如下:
之间的关系如下: ;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:

(1)计算![]() 值;
值;
(2)以此样本的频率作为概率,求
①在本次达标测试中,“喵儿”得分等于![]() 的概率;
的概率;
②“喵儿”在本次达标测试中可能得分的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本大题满分12分)
随着互联网的快速发展,基于互联网的共享单车应运而生,某市场研究人员为了了解共享单车运营公司![]() 的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图:
的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图:

(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率![]() 与月份代码
与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 公司2017年4月的市场占有率;
公司2017年4月的市场占有率;
(Ⅱ)为进一步扩大市场,公司拟再采购一批单车,现有采购成本分别为![]() 元/辆和1200元/辆的
元/辆和1200元/辆的![]() 、
、![]() 两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致单车使用寿命各不相同,考虑到公司运营的经济效益,该公司决定先对这两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命的频数表如下:
两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致单车使用寿命各不相同,考虑到公司运营的经济效益,该公司决定先对这两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命的频数表如下:
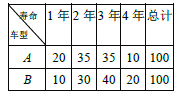
经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率,如果你是![]() 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考公式:回归直线方程为![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,则关于
,则关于![]() 的方程
的方程![]() ,给出下列五个命题:①存在实数
,给出下列五个命题:①存在实数![]() ,使得该方程没有实根;
,使得该方程没有实根;
②存在实数![]() ,使得该方程恰有
,使得该方程恰有![]() 个实根;
个实根;
③存在实数![]() ,使得该方程恰有
,使得该方程恰有![]() 个不同实根;
个不同实根;
④存在实数![]() ,使得该方程恰有
,使得该方程恰有![]() 个不同实根;
个不同实根;
⑤存在实数![]() ,使得该方程恰有
,使得该方程恰有![]() 个不同实根.
个不同实根.
其中正确的命题的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com