
【题目】已知函数f(x)=ax﹣1﹣lnx(a∈R).
(1)当a=1时,求曲线在点(1,0)处的切线方程;
(2)求函数f(x)在区间 ![]() 上的最小值.
上的最小值.
【答案】
(1)解:函数f(x)的定义域为(0,+∞),
当a=1时,f′(x)=1﹣ ![]() ,则f'(1)=0,故曲线在点(1,0)处的切线为y=0
,则f'(1)=0,故曲线在点(1,0)处的切线为y=0
(2)解:f′(x)= ![]() (x>0),则:
(x>0),则:
①当a≤0时,f'(x)<0,
此时f(x)在[ ![]() ,2]上单减,故f(x)min=f(2)=2a﹣1﹣ln2
,2]上单减,故f(x)min=f(2)=2a﹣1﹣ln2
②当a>0时,
(Ⅰ)0< ![]() ≤
≤ ![]() ,即a≥2,f(x)在上单增,故f(x)min=f(
,即a≥2,f(x)在上单增,故f(x)min=f( ![]() )=
)= ![]() ﹣1+ln2;
﹣1+ln2;
(Ⅱ) ![]() <
< ![]() <2,即
<2,即 ![]() <a<2,f(x)在[
<a<2,f(x)在[ ![]() ,
, ![]() )单减,在[
)单减,在[ ![]() ,2]单增,故f(x)min=f(
,2]单增,故f(x)min=f( ![]() )=lna.
)=lna.
(Ⅲ) ![]() ≥2,即0<a≤
≥2,即0<a≤ ![]() ,f(x)在[
,f(x)在[ ![]() ,2]上单减,故f(x)min=f(2)=2a﹣1﹣ln2,
,2]上单减,故f(x)min=f(2)=2a﹣1﹣ln2,
综上f(x)min= 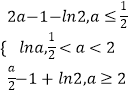
【解析】(1)利用导数与曲线斜率的公式即可求得结论;(2)分类讨论,利用导数即可求得函数的最小值.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知长方体ABCD﹣A1B1C1D1中,底面ABCD为正方形,DD1⊥平面ABCD,AB=4,AA1=2,点E1在棱C1D1上,且D1E1=3.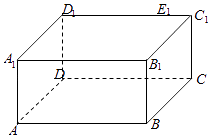
(Ⅰ)在棱CD上确定一点E,使得直线EE1∥平面D1DB,并写出证明过程;
(Ⅱ)若动点F在正方形ABCD内,且AF=2,请说明点F的轨迹,探求E1F长度的最小值并求此时直线E1F与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点p(x,y)是直线kx+y+4=0(k>0)上一动点,PA、PB是圆C:x2+y2﹣2y=0的两条切线,A、B是切点,若四边形PACB的最小面积是2,则k的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)(x∈R)的图象如图所示,f′(x)是f(x)的导函数,则不等式(x﹣1)f′(x)<0的解集为( ) 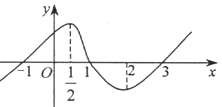
A.(﹣∞, ![]() )∪(1,2)
)∪(1,2)
B.(﹣1,1)∪(1,3)
C.(﹣1, ![]() )∪(3,+∞)
)∪(3,+∞)
D.(﹣∞,﹣1)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题: 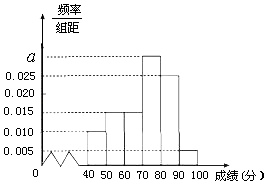
(1)求a并估计这次考试中该学科的中位数、平均值;
(2)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组…第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差不小于30分(以分数段为依据,不以具体学生分数为依据,如:[40,50),[70,80)这两组分数之差为30分),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com