练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (本小题满分12分) 已知二次函数满足条件，及.
    （1）求的解析式；（2）求在上的最大和最小值.

    （1）；（2），。

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）计算：
    （1）0.25×-4÷；
    （2）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知,,其中是自然常数）.
    （Ⅰ）求的单调性和极小值；
    （Ⅱ）求证：在上单调递增；
    （Ⅲ）求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某同学利用暑假时间到一家商场勤工俭学，该商场向他提供了三种付款方式：第一种，每天支付38圆；第二种，第一天付4元，第二天付8元，第三天付12元，以此类推：第三种，第一天付0.4元，以后每天比前一天翻一番（即增加一倍），
    你会选择哪种方式领取报酬呢？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分12分)
    已知某食品厂需要定期购买食品配料，该厂每天需要食品配料200千克，配料的价格为元/千克，每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用（若天购买一次，需要支付天的保管费）。其标准如下: 7天以内（含7天），无论重量多少，均按10元/天支付；超出7天以外的天数，根据实际剩余配料的重量，以每天0.03元/千克支付.
    (1）当9天购买一次配料时，求该厂用于配料的保管费用是多少元？[
    (2）设该厂天购买一次配料，求该厂在这天中用于配料的总费用（元）关于的函数关系式，并求该厂多少天购买一次配料才能使平均每天支付的费用最少?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知二次函数在处取得极值，且在点处的切线与直线平行． 
    (1）求的解析式；      (2）求函数的单调递增区间及极值；
    (3）求函数在的最值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数
    （1）当时，求函数的最大值和最小值；   
    （2）求实数的取值范围，使在区间上是单调函数。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分12分）
    某公司生产一种电了仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：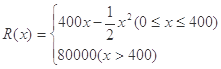
      ，其中是仪器的月产量。
    ⑴将利润表示为月产量的函数。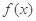
    ⑵当月产量为何值时，公司所获利润最大？最大利润为多少元？（总收益―总成本＝利润）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分12分)
    某出版社新出版一本高考复习用书，该书的成本为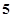元一本，经销过程中每本书需付给代理商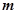元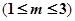的劳务费，经出版社研究决定，新书投放市场后定价为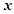元一本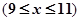，，预计一年的销售量为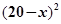万本.
    （Ⅰ）求该出版社一年的利润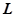（万元）与每本书的定价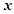的函数关系式；
    （Ⅱ）若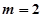时，当每本书的定价为多少元时，该出版社一年利润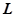最大，并求出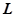的最大值.

    查看答案和解析>>

    同步练习册答案