
【题目】某三棱锥的三视图如图所示,该三棱锥的表面积是 .

【答案】30+6![]()
【解析】
试题分析:根据三视图,可得该三棱锥为如图的三棱锥A﹣BCD,其中底面△BCD中,CD⊥BC,且侧面ABC与底面ABC互相垂直,由此结合题中的数据结合和正余弦定理,不难算出该三棱锥的表面积.
解:根据题意,还原出如图的三棱锥A﹣BCD
底面Rt△BCD中,BC⊥CD,且BC=5,CD=4
侧面△ABC中,高AE⊥BC于E,且AE=4,BE=2,CE=3
侧面△ACD中,AC=![]() =5
=5
∵平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,AE⊥BC
∴AE⊥平面BCD,结合CD平面BCD,得AE⊥CD
∵BC⊥CD,AE∩BC=E
∴CD⊥平面ABC,结合AC平面ABC,得CD⊥AC
因此,△ADB中,AB=![]() =2
=2![]() ,BD=
,BD=![]() =
=![]() ,AD=
,AD=![]() =
=![]() ,
,
∴cos∠ADB=![]() =
=![]() ,得sin∠ADB=
,得sin∠ADB=![]() =
=![]()
由三角形面积公式,得S△ADB=![]() ×
×![]() ×
×![]() ×
×![]() =6
=6![]()
又∵S△ACB=![]() ×5×4=10,S△ADC=S△CBD=
×5×4=10,S△ADC=S△CBD=![]() ×4×5=10
×4×5=10
∴三棱锥的表面积是S表=S△ADB+S△ADC+S△CBD+S△ACB=30+6![]()
故答案为:30+6![]()



 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】若曲线C上任意一点与直线![]() 上任意一点的距离都大于1,则称曲线C远离”直线
上任意一点的距离都大于1,则称曲线C远离”直线![]() ,在下列曲线中,“远离”直线
,在下列曲线中,“远离”直线![]() :y=2x的曲线有___________(写出所有符合条件的曲线的编号)
:y=2x的曲线有___________(写出所有符合条件的曲线的编号)
①曲线C:![]() ;②曲线C:
;②曲线C:![]() ;③曲线C:
;③曲线C:![]() ;
;
④曲线C:![]() ;⑤曲线C:
;⑤曲线C:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在推导很多三角恒等变换公式时,我们可以利用平面向量的有关知识来研究,在一定程度上可以简化推理过程.如我们就可以利用平面向量来推导两角差的余弦公式:![]()
具体过程如下:
如图,在平面直角坐标系![]() 内作单位圆O,以
内作单位圆O,以![]() 为始边作角
为始边作角![]() .它们的终边与单位圆O的交点分别为A,B.
.它们的终边与单位圆O的交点分别为A,B.

则![]()
由向量数量积的坐标表示,有:
![]()
设![]() 的夹角为θ,则
的夹角为θ,则
![]()
另一方面,由图3.1—3(1)可知,![]() ;由图可知,
;由图可知,

![]() .于是
.于是![]() .
.
所以![]() ,也有
,也有![]() ,
,
所以,对于任意角![]() 有:
有:![]() (
(![]() )
)
此公式给出了任意角![]() 的正弦、余弦值与其差角
的正弦、余弦值与其差角![]() 的余弦值之间的关系,称为差角的余弦公式,简记作
的余弦值之间的关系,称为差角的余弦公式,简记作![]() .
.
有了公式![]() 以后,我们只要知道
以后,我们只要知道![]() 的值,就可以求得
的值,就可以求得![]() 的值了.
的值了.
阅读以上材料,利用下图单位圆及相关数据(图中M是AB的中点),采取类似方法(用其他方法解答正确同等给分)解决下列问题:
(1)判断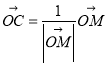 是否正确?(不需要证明)
是否正确?(不需要证明)
(2)证明:![]()
(3)利用以上结论求函数![]() 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
项目 员工 | A | B | C | D | E | F |
子女教育 | ○ | ○ | × | ○ | × | ○ |
继续教育 | × | × | ○ | × | ○ | ○ |
大病医疗 | × | × | × | ○ | × | × |
住房贷款利息 | ○ | ○ | × | × | ○ | ○ |
住房租金 | × | × | ○ | × | × | × |
赡养老人 | ○ | ○ | × | × | × | ○ |
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中, ![]() 底面
底面![]() ,
,![]() .
. ![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点.
的中点. ![]() 为侧棱
为侧棱![]() 上的动点.
上的动点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)试判断直线![]() 与平面
与平面![]() 是否能够垂直.若能垂直,求
是否能够垂直.若能垂直,求![]() 的值;若不能垂直,请说明理由.
的值;若不能垂直,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有一特色酒店由一些完全相同的帐篷构成.每座帐篷的体积为![]() 立方米,且分上下两层,其中上层是半径为
立方米,且分上下两层,其中上层是半径为![]() (单位:米)的半球体,下层是半径为
(单位:米)的半球体,下层是半径为![]() 米,高为
米,高为![]() 米的圆柱体(如图).经测算,上层半球体部分每平方米建造费用为2千元,下方圆柱体的侧面、隔层和地面三个部分平均每平方米建造费用为3千元,设每座帐篷的建造费用为
米的圆柱体(如图).经测算,上层半球体部分每平方米建造费用为2千元,下方圆柱体的侧面、隔层和地面三个部分平均每平方米建造费用为3千元,设每座帐篷的建造费用为![]() 千元.
千元.
参考公式:球的体积![]() ,球的表面积
,球的表面积![]() ,其中
,其中![]() 为球的半径.
为球的半径.

(1)求![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)当半径![]() 为何值时,每座帐篷的建造费用最小,并求出最小值.
为何值时,每座帐篷的建造费用最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估计该校学生每周平均体育运动时间超过4小时的概率.

(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com