
【题目】某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
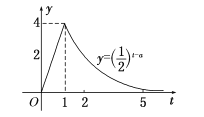
(1)写出第一次服药后,y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.求服药一次后治疗有效的时间是多长?
【答案】(1)![]() ; (2)服药一次后治疗有效的时间是5-
; (2)服药一次后治疗有效的时间是5-![]() =
=![]() 小时.
小时.
【解析】
(1)由函数图象的奥这是一个分段函数,第一段为正比例函数的一段,第二段是指数函数的一段,由于两端函数均过点![]() ,代入点
,代入点![]() 的坐标,求出参数的值,即可得到函数的解析式;
的坐标,求出参数的值,即可得到函数的解析式;
(2)由(1)的结论将函数值![]() 代入函数的解析式,构造不等式,求出每毫升血液中函数不少于
代入函数的解析式,构造不等式,求出每毫升血液中函数不少于![]() 微克的起始时刻和结束时刻,即可得到结论.
微克的起始时刻和结束时刻,即可得到结论.
(1)由题意,根据给定的函数的图象,可设函数的解析式为 ,
,
又由函数的图象经过点![]() ,
,
则当![]() 时,
时,![]() ,解得
,解得![]() ,
,
又由![]() 时,
时,![]() ,解得
,解得![]() ,
,
所以函数的解析式为 .
.
(2)由题意,令![]() ,即当
,即当![]() 时,
时,![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
综上所述,可得实数![]() 的取值范围是
的取值范围是![]() ,
,
所以服药一次后治疗有效的时间是![]() 小时.
小时.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某果农选取一片山地种植红柚,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:![]() ),获得的所有数据按照区间
),获得的所有数据按照区间![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到频率分布直方图如图。已知样本中产量在区间
进行分组,得到频率分布直方图如图。已知样本中产量在区间![]() 上的果树株数是产量在区间
上的果树株数是产量在区间![]() 上的果树株数的
上的果树株数的![]() 倍。
倍。
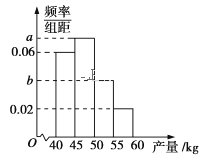
(1)求![]() 的值;
的值;
(2)求样本的平均数和中位数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,点
中,点![]() 是
是![]() 的中点,欲过点
的中点,欲过点![]() 作一截面与平面
作一截面与平面![]() 平行.
平行.
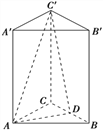
(I)问应当怎样画线,并说明理由;
(II)求所作截面与平面![]() 将三棱柱分成的三部分的体积之比.
将三棱柱分成的三部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“砥砺奋进的五年”,首都经济社会发展取得新成就.自2012年以来,北京城乡居民收入稳步增长.随着扩大内需,促进消费等政策的出台,居民消费支出全面增长,消费结构持续优化升级,城乡居民人均可支配收入快速增长,人民生活品质不断提升.下图是北京市2012-2016年城乡居民人均可支配收入实际增速趋势图(例如2012年,北京城镇居民收入实际增速为7.3%,农村居民收入实际增速为8.2%).
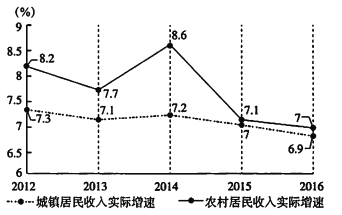
(Ⅰ)从2012-2016五年中任选一年,求城镇居民收入实际增速大于7%的概率;
(Ⅱ)从2012-2016五年中任选一年,求至少有一年农村和城镇居民收入实际增速均超过7%的概率;
(Ⅲ)由图判断,从哪年开始连续三年农村居民收入实际增速方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,离心率
,离心率![]() .
.
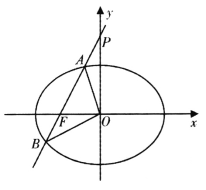
(I)求椭圆C的标准方程;
(II)已知直线![]() 交椭圆C于A,B两点.
交椭圆C于A,B两点.
①若直线![]() 经过椭圆C的左焦点F,交y轴于点P,且满足
经过椭圆C的左焦点F,交y轴于点P,且满足![]() .求证:
.求证:![]() 为定值;
为定值;
②若![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com