
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() .
.
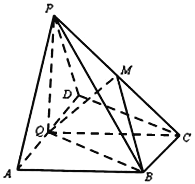
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 为棱
为棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)若二面角![]() 大小为
大小为![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意先证明![]() ,由面面垂直的性质定理得
,由面面垂直的性质定理得![]() 平面
平面![]() ,再运用面面垂直的判定定理证明
,再运用面面垂直的判定定理证明
(2)以![]() 为原点建立空间直角坐标系,求出直线
为原点建立空间直角坐标系,求出直线![]() 与
与![]() 的向量表示,然后运用空间向量知识求出异面直线所成角的余弦值
的向量表示,然后运用空间向量知识求出异面直线所成角的余弦值
(3)结合(2)中的空间直角坐标系,运用向量知识结合二面角为![]() 求出结果
求出结果
(1)证明:![]() 为
为![]() 的中点,
的中点,
∴四边形![]() 为平行四边形,
为平行四边形,
![]()
![]() 即
即![]()
又![]() 平面
平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
∵![]() 平面
平面![]() , ∴平面
, ∴平面![]() 平面
平面![]()
(2)解:![]() 为
为![]() 的中点,
的中点,
![]()
∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
如图,以![]() 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
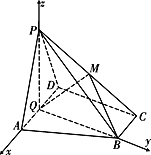
则![]() ,
,
![]() 是
是![]() 的中点,
的中点,![]()
![]()
设异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,
则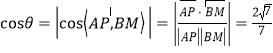
∴异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(3)解:由(2)知平面![]() 的法向量为
的法向量为![]()
由![]()
得![]()
又![]() ,
,
设平面![]() 法向量为
法向量为![]() ,
,
由![]() 可取
可取![]()
∵二面角![]() 为60°,
为60°,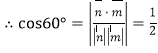 ,
,
![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点为
的一个焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程与离心率;
的方程与离心率;
(Ⅱ)设椭圆![]() 上不与
上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长是定值.
轴截得的弦长是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,PA=PD,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F.

(1)求证:EF∥平面PAB;
(2)若PB与平面ABCD所成角的正弦值为![]() ,求二面角P-AE-B的余弦值.
,求二面角P-AE-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+![]() .
.
(1)若关于x的不等式f(3x)≤m3x+2在[-2,2]上恒成立.求实数m的取值范围;
(2)若函数g(x)=f(|2x-1|)![]() -3t-2有四个不同的零点,求实数t的取值范围.
-3t-2有四个不同的零点,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试用恰当的方法表示下列集合.
(1)使函数![]() 有意义的x的集合;
有意义的x的集合;
(2)不大于12的非负偶数;
(3)满足不等式![]() 的解集;
的解集;
(4)由大于10小于20的所有整数组成的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了加强中学生实践、创新和团队建设能力的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表,解答下列问题:
(1)完成频率分布表(直接写出结果);
(2)若成绩在90.5分以上的学生获一等奖,试估计全校获一等奖的人数,现在从全校所有获一等奖的同学中随机抽取2名同学代表学校参加竞赛,某班共有2名同学荣获一等奖,求该班同学恰有1人参加竞赛的概率.
分组 | 频数 | 频率 | |
第1组 | [60.5,70.5) | 0.26 | |
第2组 | [70.5,80.5) | 17 | |
第3组 | [80.5,90.5) | 18 | 0.36 |
第4组 | [90.5,100.5] | ||
合计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).

(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园内有一块边长为![]() 的正三角形
的正三角形![]() 空地,拟改建成花园,并在其中建一直道
空地,拟改建成花园,并在其中建一直道![]() 方便花园管理. 设
方便花园管理. 设![]() 分别在
分别在![]() 上,且
上,且![]() 均分三角形
均分三角形![]() 的面积.
的面积.
(1)设![]() (
(![]() ),
),![]() ,试将
,试将![]() 表示为
表示为![]() 的函数关系式;
的函数关系式;
(2)若![]() 是灌溉水管,为节约成本,希望其最短,
是灌溉水管,为节约成本,希望其最短,![]() 的位置应在哪里?若
的位置应在哪里?若![]() 是参观路线,希望其最长,
是参观路线,希望其最长,![]() 的位置应在哪里?
的位置应在哪里?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com