
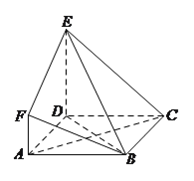
【题目】如图,在四棱锥A﹣BCFE中,四边形EFCB为梯形,EF∥BC,且EF= ![]() BC,△ABC是边长为2的正三角形,顶点F在AC上的射影为点G,且FG=
BC,△ABC是边长为2的正三角形,顶点F在AC上的射影为点G,且FG= ![]() ,CF=
,CF= ![]() ,BF=
,BF= ![]() .
. 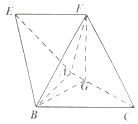
(1)证明:平面FGB⊥平面ABC;
(2)求二面角E﹣AB﹣F的余弦值.
【答案】
(1)证明:由顶点F在AC上投影为点G,可知,FG⊥AC.
取AC的中点为O,连结OB,GB.
在Rt△FGC中, ![]() ,
, ![]() ,所以
,所以 ![]() .
.
在Rt△GBO中, ![]() ,
, ![]() ,所以
,所以 ![]() .
.
所以,BG2+GF2=FB2,即FG⊥BG.
∵FG⊥AC,FG⊥GB,AC∩BG=G
∴FG⊥面ABC.
又FG面FGB,所以面FGB⊥面ABC
(2)解:由(Ⅰ)知,OB⊥FG,OB⊥AC,且AC∩FG=G
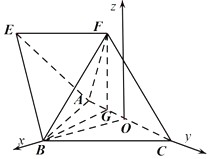
所以 OB⊥面AFC,且FG⊥面ABC.以OB所在直线为x轴,OC所在直线为y轴,
过点O作平面ABC的垂线为z轴,建立空间直角坐标系,如图所示:
![]() ,
, ![]() ,
,
![]() ,
, ![]() =(0,﹣
=(0,﹣ ![]() ,
, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ),
),
设平面ABE,ABF的法向量分别为 ![]() ,
, ![]() ,
,
则 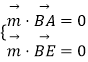 ,即
,即 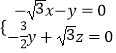 ,取x=1,得
,取x=1,得 ![]() =(1,﹣
=(1,﹣ ![]() ,﹣
,﹣ ![]() ),
),
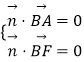 ,即
,即 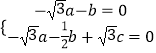 ,取a=1,得
,取a=1,得 ![]() ,
,
设二面角E﹣AB﹣F的平面角为θ.
则cosθ= 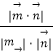 =
= ![]() =
= ![]() .
.
所以二面角E﹣AB﹣F的余弦值为 ![]() .
.
【解析】(1)推导出FG⊥AC,取AC的中点为O,连结OB,GB,推导出FG⊥BG,FG⊥AC,从而FG⊥面ABC,由此能证明面FGB⊥面ABC.(2)以OB所在直线为x轴,OC所在直线为y轴,过点O作平面ABC的垂线为z轴,建立空间直角坐标系,利用向量法能求出二面角E﹣AB﹣F的余弦值.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]()
(1)求证:直线![]() 过定点;
过定点;
(2)求直线![]() 被圆
被圆![]() 所截得的弦长最短时
所截得的弦长最短时![]() 的值;
的值;
(3)已知点![]() ,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有
,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有![]() 为一常数,试求所有满足条件的点N的坐标及该常数.
为一常数,试求所有满足条件的点N的坐标及该常数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.

根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年我国将加快阶梯水价推行,原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变.为响应国家政策,制定合理的阶梯用水价格,某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研,抽取的数据的茎叶图如下(单位:吨):

(1)在郊区的这5户居民中随机抽取2户,求其年人均用水量都不超过30吨的概率;
(2)设该城市郊区和城区的居民户数比为![]() ,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一梯次的居民用户用水价格保持不变.试根据样本估计总体的思想,分析此方案是否符合国家“保基本”政策.
,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一梯次的居民用户用水价格保持不变.试根据样本估计总体的思想,分析此方案是否符合国家“保基本”政策.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 内一点
内一点![]() ,直线
,直线![]() 过点
过点![]() 且与圆
且与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求圆![]() 的圆心坐标和面积;
的圆心坐标和面积;
(2)若直线![]() 的斜率为
的斜率为![]() ,求弦
,求弦![]() 的长;
的长;
(3)若圆上恰有三点到直线![]() 的距离等于
的距离等于![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较注射![]() 两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .
.
(1)甲、乙是200只家兔中的2只,求甲、乙分在不同组的概率;
(2)下表1和表2分别是注射药物![]() 和
和![]() 后的试验结果.(疱疹面积单位:
后的试验结果.(疱疹面积单位: ![]() )
)
表1:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表

表2:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表

(ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
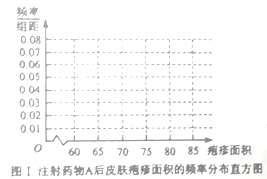
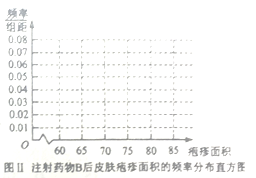
(ⅱ)完成下面![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“注射药物
的把握认为“注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 后的疱疹面积有差异”.
后的疱疹面积有差异”.
表3:

附: 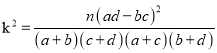
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)设点![]() 是线段
是线段![]() 上一个动点,试确定点
上一个动点,试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)经过点(﹣1,
=1(a>b>0)经过点(﹣1, ![]() ),其离心率e=
),其离心率e= ![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设动直线l:y=kx+m与椭圆C相切,切点为T,且l与直线x=﹣4相交于点S.
试问:在x轴上是否存在一定点,使得以ST为直径的圆恒过该定点?若存在,求出该点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com