
ЁОЬтФПЁПФГИпМЖжабЇНёФъИпвЛФъМЖеаЪеЁАЙњМЪАрЁБбЇЩњ![]() ШЫЃЌбЇаЃЮЊетаЉбЇЩњПЊБйСЫжБЩ§КЃЭтвЛСїДѓбЇЕФТЬЩЋЭЈЕРЃЌЮЊСЫж№ВНЬсИпетаЉбЇЩњгыЙњМЪНЬг§НгЙьЕФФмСІЃЌНЋет
ШЫЃЌбЇаЃЮЊетаЉбЇЩњПЊБйСЫжБЩ§КЃЭтвЛСїДѓбЇЕФТЬЩЋЭЈЕРЃЌЮЊСЫж№ВНЬсИпетаЉбЇЩњгыЙњМЪНЬг§НгЙьЕФФмСІЃЌНЋет![]() ШЫЗжЮЊШ§ИіХњДЮВЮМгЙњМЪНЬг§бааоХрбЕЃЌдкетШ§ИіХњДЮЕФбЇЩњжаФаЁЂХЎбЇЩњШЫЪ§ШчЯТБэЃК
ШЫЗжЮЊШ§ИіХњДЮВЮМгЙњМЪНЬг§бааоХрбЕЃЌдкетШ§ИіХњДЮЕФбЇЩњжаФаЁЂХЎбЇЩњШЫЪ§ШчЯТБэЃК
ЕквЛХњДЮ | ЕкЖўХњДЮ | ЕкШ§ХњДЮ | |
ХЎ |
|
|
|
Фа |
|
|
|
вбжЊдкет![]() УћбЇЩњжаЫцЛњГщШЁ
УћбЇЩњжаЫцЛњГщШЁ![]() УћЃЌГщЕНЕквЛХњДЮЁЂЕкЖўХњДЮжаХЎбЇЩњЕФИХТЪЗжБ№ЪЧ
УћЃЌГщЕНЕквЛХњДЮЁЂЕкЖўХњДЮжаХЎбЇЩњЕФИХТЪЗжБ№ЪЧ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЮЊСЫМьбщбааоЕФаЇЙћЃЌЯжДгШ§ИіХњДЮжаАДЗжВуГщбљЕФЗНЗЈГщШЁ![]() УћЭЌбЇЮЪОэЕїВщЃЌдђШ§ИіХњДЮБЛбЁШЁЕФШЫЪ§ЗжБ№ЪЧЖрЩйЃП
УћЭЌбЇЮЪОэЕїВщЃЌдђШ§ИіХњДЮБЛбЁШЁЕФШЫЪ§ЗжБ№ЪЧЖрЩйЃП
ЃЈ3ЃЉШєДгЕкЃЈ2ЃЉаЁЮЪбЁШЁЕФбЇЩњжаЫцЛњбЁГіСНУћбЇЩњНјааЗУЬИЃЌЧѓЁАВЮМгЗУЬИЕФСНУћЭЌбЇжСЩйгавЛИіШЫРДздЕквЛХњДЮЁБЕФИХТЪ.
ЁОД№АИЁП(1)![]() ЃЛ(2)
ЃЛ(2)![]() ЃЛ(3)
ЃЛ(3)![]() .
.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉгЩЬтвтНсКЯЫљИјЕФЪ§ОнМЦЫуПЩЕУ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЬтвтНсКЯЗжВуГщбљБШМЦЫуПЩЕУЕквЛХњДЮЃЌЕкЖўХњДЮЃЌЕкШ§ХњДЮБЛГщШЁЕФШЫЪ§ЗжБ№ЮЊ![]()
ЃЈ3ЃЉЩшЕквЛХњДЮбЁШЁЕФШ§ИібЇЩњЩшЮЊ![]() ЕкЖўХњДЮбЁШЁЕФбЇЩњЮЊ
ЕкЖўХњДЮбЁШЁЕФбЇЩњЮЊ![]()
![]() ЃЌЕкШ§ХњДЮбЁШЁЕФбЇЩњЮЊ
ЃЌЕкШ§ХњДЮбЁШЁЕФбЇЩњЮЊ![]() ЃЌРћгУСаОйЗЈПЩЕУДгет
ЃЌРћгУСаОйЗЈПЩЕУДгет![]() УћбЇдБжаЫцЛњбЁГіСНУћбЇдБЕФЫљгаЛљБОЪТМўЮЊ
УћбЇдБжаЫцЛњбЁГіСНУћбЇдБЕФЫљгаЛљБОЪТМўЮЊ![]() ИіЃЌЁАСНУћЭЌбЇжСЩйгавЛИіРДздЕквЛХњДЮЁБЕФЪТМўАќРЈЙВ
ИіЃЌЁАСНУћЭЌбЇжСЩйгавЛИіРДздЕквЛХњДЮЁБЕФЪТМўАќРЈЙВ![]() ИіЃЌгЩЙХЕфИХаЭМЦЫуЙЋЪНПЩЕУЯргІЕФИХТЪжЕЮЊ
ИіЃЌгЩЙХЕфИХаЭМЦЫуЙЋЪНПЩЕУЯргІЕФИХТЪжЕЮЊ![]() .
.
ЯъНтЃКЃЈ1ЃЉ![]()
![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЬтвтжЊЃЌЕквЛХњДЮЃЌЕкЖўХњДЮЃЌЕкШ§ХњДЮЕФШЫЪ§ЗжБ№ЪЧ![]()
![]()
ЫљвдЕквЛХњДЮЃЌЕкЖўХњДЮЃЌЕкШ§ХњДЮБЛГщШЁЕФШЫЪ§ЗжБ№ЮЊ![]()
ЃЈ3ЃЉЕквЛХњДЮбЁШЁЕФШ§ИібЇЩњЩшЮЊ![]() ЕкЖўХњДЮбЁШЁЕФбЇЩњЮЊ
ЕкЖўХњДЮбЁШЁЕФбЇЩњЮЊ![]()
![]() ЃЌЕкШ§ХњДЮбЁШЁЕФбЇЩњЮЊ
ЃЌЕкШ§ХњДЮбЁШЁЕФбЇЩњЮЊ![]() ЃЌдђДгет
ЃЌдђДгет![]() УћбЇдБжаЫцЛњбЁГіСНУћбЇдБЕФЫљгаЛљБОЪТМўЮЊЃК
УћбЇдБжаЫцЛњбЁГіСНУћбЇдБЕФЫљгаЛљБОЪТМўЮЊЃК
![]() ЙВ
ЙВ![]() ИіЃЌ
ИіЃЌ
ЁАСНУћЭЌбЇжСЩйгавЛИіРДздЕквЛХњДЮЁБЕФЪТМўАќРЈЃК
![]() ЙВ
ЙВ![]() ИіЃЌ
ИіЃЌ
ЫљвдЁАСНУћЭЌбЇжСЩйгавЛИіРДздЕквЛХњДЮЁБЕФИХТЪ![]() .
.


 аЧМЖПкЫуЬьЬьСЗЯЕСаД№АИ
аЧМЖПкЫуЬьЬьСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОдкгаТФъЭэЛсЩЯОйааГщНБЛюЖЏЃЌгаМзЁЂввСНИіГщНБЗНАИЙЉдБЙЄбЁдёЃЛ
ЗНАИМзЃКдБЙЄзюЖргаСНДЮГщНБЛњЛсЃЌУПДЮГщНБЕФжаНБТЪЮЊ ![]() .ЕквЛДЮГщНБЃЌШєЮДжаНБЃЌдђГщНБНсЪј.ШєжаНБЃЌдђЭЈЙ§ХзвЛУЖжЪЕиОљдШЕФгВБвЃЌОіЖЈЪЧЗёМЬајНјааЕкЖўДЮГщНБЃЌЙцЖЈЃКШєХзГігВБвЃЌЗДУцГЏЩЯЃЌдБЙЄдђЛёЕУ500дЊНБН№ЃЌВЛНјааЕкЖўДЮГщНБЃЛШєе§УцГЏЩЯЃЌдБЙЄдђаыНјааЕкЖўДЮГщНБЃЌЧвдкЕкЖўДЮГщНБжаЃЌШєжаНБЃЌЛёЕУНБН№1000дЊЃЛШєЮДжаНБЃЌдђЫљЛёНБН№ЮЊ0дЊ.
.ЕквЛДЮГщНБЃЌШєЮДжаНБЃЌдђГщНБНсЪј.ШєжаНБЃЌдђЭЈЙ§ХзвЛУЖжЪЕиОљдШЕФгВБвЃЌОіЖЈЪЧЗёМЬајНјааЕкЖўДЮГщНБЃЌЙцЖЈЃКШєХзГігВБвЃЌЗДУцГЏЩЯЃЌдБЙЄдђЛёЕУ500дЊНБН№ЃЌВЛНјааЕкЖўДЮГщНБЃЛШєе§УцГЏЩЯЃЌдБЙЄдђаыНјааЕкЖўДЮГщНБЃЌЧвдкЕкЖўДЮГщНБжаЃЌШєжаНБЃЌЛёЕУНБН№1000дЊЃЛШєЮДжаНБЃЌдђЫљЛёНБН№ЮЊ0дЊ.
ЗНАИввЃКдБЙЄСЌајШ§ДЮГщНБЃЌУПДЮжаНБТЪОљЮЊ ![]() ЃЌУПДЮжаНБОљПЩЛёНБН№400дЊ.
ЃЌУПДЮжаНБОљПЩЛёНБН№400дЊ.
ЃЈ1ЃЉЧѓФГдБЙЄбЁдёЗНАИМзНјааГщНБЫљЛёНБН№ ![]() ЃЈдЊЃЉЕФЗжВМСаЃЛ
ЃЈдЊЃЉЕФЗжВМСаЃЛ
ЃЈ2ЃЉФГдБЙЄбЁдёЗНАИввгыбЁдёЗНАИМзНјааГщНБЃЌЪдБШНЯФФИіЗНАИИќЛЎЫуЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌвдзјБъдЕуЮЊМЋЕуЃЌ ![]() жсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎвбжЊЕу
жсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎвбжЊЕу ![]() ЕФМЋзјБъЮЊ
ЕФМЋзјБъЮЊ ![]() ЃЌжБЯп
ЃЌжБЯп ![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ ![]() ЃЌЧвЕу
ЃЌЧвЕу ![]() дкжБЯп
дкжБЯп ![]() ЩЯЃЎ
ЩЯЃЎ
ЃЈ1ЃЉЧѓ ![]() ЕФжЕМАжБЯп
ЕФжЕМАжБЯп ![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉдВ ![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ ![]() ЃЌЪдХаЖЯжБЯп
ЃЌЪдХаЖЯжБЯп ![]() гыдВ
гыдВ ![]() ЕФЮЛжУЙиЯЕЃЎ
ЕФЮЛжУЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉ=|x+ ![]() |+|xЉa|ЃЈaЃО0ЃЉЃЎ
|+|xЉa|ЃЈaЃО0ЃЉЃЎ
ЃЈ1ЃЉжЄУїЃКfЃЈxЃЉЁн2ЃЛ
ЃЈ2ЃЉШєfЃЈ3ЃЉЃМ5ЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() ЕФЧАnЯюКЭЮЊ
ЕФЧАnЯюКЭЮЊ![]() ,ЧвТњзу
,ЧвТњзу![]() +n=2
+n=2![]() (nЁЪ
(nЁЪ![]() )
)
(1)жЄУї:Ъ§Са![]() ЮЊЕШБШЪ§Са,ВЂЧѓЪ§Са
ЮЊЕШБШЪ§Са,ВЂЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪН;
ЕФЭЈЯюЙЋЪН;
(2)Ъ§Са![]() Тњзу
Тњзу![]() (nЁЪ
(nЁЪ![]() ),ЦфЧАnЯюКЭЮЊ
),ЦфЧАnЯюКЭЮЊ![]() ,ЪдЧѓТњзу
,ЪдЧѓТњзу![]() +
+![]() >2018ЕФзюаЁе§ећЪ§n.
>2018ЕФзюаЁе§ећЪ§n.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊИДЪ§zТњзу|z|= ![]() ЃЌz2ЕФащВПЮЊ2ЃЎ
ЃЌz2ЕФащВПЮЊ2ЃЎ
ЃЈ1ЃЉЧѓzЃЛ
ЃЈ2ЃЉЩшzЃЌz2 ЃЌ zЉz2дкИДЦНУцЖдгІЕФЕуЗжБ№ЮЊAЃЌBЃЌCЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШ§Ртжљ![]() ЕФЕзУцЪЧе§Ш§НЧаЮЃЌВрУц
ЕФЕзУцЪЧе§Ш§НЧаЮЃЌВрУц![]() ЮЊСтаЮЃЌЧв
ЮЊСтаЮЃЌЧв![]() ЃЌЦНУц
ЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФжаЕу.
ЕФжаЕу.
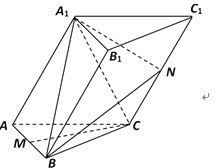
ЃЈIЃЉЧѓжЄЃК![]() ЁЮЦНУц
ЁЮЦНУц![]() ЃЛ
ЃЛ
ЃЈIIЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈIIIЃЉЧѓBA1гыЦНУц![]() ЫљГЩНЧЕФДѓаЁЃЎ
ЫљГЩНЧЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋвЛПХжЪЕиОљдШЕФе§ЗНЬхїЛзг(СљИіУцЕФЕуЪ§ЗжБ№ЮЊ1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6)ЯШКѓХзСНДЮЃЌМЧЕквЛДЮГіЯжЕФЕуЪ§ЮЊ ![]() ЃЌЕкЖўДЮГіЯжЕФЕуЪ§ЮЊ
ЃЌЕкЖўДЮГіЯжЕФЕуЪ§ЮЊ ![]() ЃЌдђЪТМўЁА
ЃЌдђЪТМўЁА ![]() ЁБЕФИХТЪЮЊ( )
ЁБЕФИХТЪЮЊ( )
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВCЕФжааФдкдЕуЃЌвЛИіНЙЕуFЃЈЉ2ЃЌ0ЃЉЃЌЧвГЄжсГЄгыЖЬжсГЄЕФБШЪЧ ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЭждВCЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшЕуMЃЈmЃЌ0ЃЉдкЭждВCЕФГЄжсЩЯЃЌЕуPЪЧЭждВЩЯШЮвтвЛЕуЃЎЕБ ![]() зюаЁЪБЃЌЕуPЧЁКУТфдкЭждВЕФгвЖЅЕуЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
зюаЁЪБЃЌЕуPЧЁКУТфдкЭждВЕФгвЖЅЕуЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com