
【题目】设函数![]() .
.
(1)若函数![]() 在区间
在区间![]() (
(![]() 为自然对数的底数)上有唯一的零点,求实数
为自然对数的底数)上有唯一的零点,求实数![]() 的取值范围;
的取值范围;
(2)若在![]() (
(![]() 为自然对数的底数)上存在一点
为自然对数的底数)上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() (2)
(2)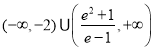 .
.
【解析】
(1)求得![]() ,对
,对![]() 的范围分类,即可判断函数
的范围分类,即可判断函数![]() 的单调性,结合
的单调性,结合![]() 即可判断函数
即可判断函数![]() 在区间
在区间![]() 上是否有唯一的零点,问题得解。
上是否有唯一的零点,问题得解。
(2)将问题转化为:函数![]() 在
在![]() 上的最小值小于零.求得
上的最小值小于零.求得![]() ,对
,对![]() 的范围分类即可判断函数的单调性,从而求得
的范围分类即可判断函数的单调性,从而求得![]() 的最小值,问题得解。
的最小值,问题得解。
(1)![]() ,其中
,其中![]() .
.
①当![]() 时,
时,![]() 恒成立,
恒成立,![]() 单调递增,
单调递增,
又∵![]() ,函数
,函数![]() 在区间
在区间![]() 上有唯一的零点,符合题意.
上有唯一的零点,符合题意.
②当![]() 时,
时,![]() 恒成立,
恒成立,![]() 单调递减,
单调递减,
又∵![]() ,函数
,函数![]() 在区间
在区间![]() 上有唯一的零点,符合题意.
上有唯一的零点,符合题意.
③当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
又∵![]() ,∴
,∴![]() ,
,
∴函数![]() 在区间
在区间![]() 有唯一的零点,
有唯一的零点,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时符合题意,即
时符合题意,即![]() ,
,
∴![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有唯一的零点;
上有唯一的零点;
∴![]() 的取值范围是
的取值范围是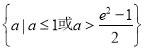 .
.
(2)在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,等价于
成立,等价于![]() 在
在![]() 上有解,即函数
上有解,即函数![]() 在
在![]() 上的最小值小于零.
上的最小值小于零.
![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 的最小值为
的最小值为![]() ,由
,由![]() 可得
可得![]() ,∵
,∵![]() ,∴
,∴![]() ;
;
②当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 的最小值为
的最小值为![]() ,由
,由![]() 可得
可得![]() ;
;
③当![]() 时,即
时,即![]() 时,
时,
可得![]() 的最小值为
的最小值为![]() ,∵
,∵![]() ,∴
,∴![]() ,
,![]() ,所以
,所以![]() 不成立.
不成立.
综上所述:可得所求![]() 的取值范围是
的取值范围是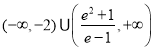 .
.


科目:高中数学 来源: 题型:
【题目】某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算该项目月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似地表示为:
(吨)之间的函数关系可以近似地表示为:
 ,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.
,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.
(1)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是元代著名数学家,他所著《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中提到一些堆垛问题,如“三角垛果子”,就是将一样大小的果子堆垛成正三棱锥,每层皆堆成正三角形,从上向下数,每层果子数分别为1,3,6,10,…,现有一个“三角垛果子”,其最底层每边果子数为10,则该层果子数为( )
A. 50B. 55C. 100D. 110
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 与x轴交于A,B两点,点Q的坐标为
与x轴交于A,B两点,点Q的坐标为![]() .
.
(1)是否存在b,使得![]() ,如果存在求出b值;如果不存在,说明理由;
,如果存在求出b值;如果不存在,说明理由;
(2)过A,B,Q三点的圆面积最小时,求圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.
(1)列出甲、乙两种产品满足的关系式,并画出相应的平面区域;
(2)在一个生产周期内该企业生产甲、乙两种产品各多少吨时可获得利润最大,最大利润是多少?
(用线性规划求解要画出规范的图形及具体的解答过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就,在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
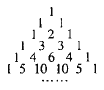
A. 110B. 114C. 124D. 125
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点的直线与椭圆![]() 交于
交于![]() 两点(
两点(![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,直线
,直线![]() 与
与![]() 轴
轴![]() 轴分别交于
轴分别交于![]() 两点.
两点.
①设直线![]() 斜率分别为
斜率分别为![]() ,证明存在常数
,证明存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值;
的值;
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com