
【题目】下列各图中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB//平面MNP的图形的序号是( )
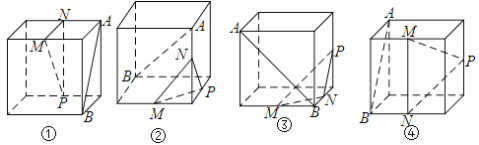
A.①③B.②③C.①④D.②④
科目:高中数学 来源: 题型:
【题目】(1)求证: ![]() .
.
(2)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
sin213°+cos217°-sin13°cos17°;
sin215°+cos215°-sin15°cos15°;
sin218°+cos212°-sin18°cos12°;
sin2(-18°)+cos248°-sin(-18°)cos48°;
sin2(-25°)+cos255°-sin(-25°)cos55°.
①试从上述五个式子中选择一个,求出这个常数;
②根据①的计算结果,将该同学的发现推广为三角恒等式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴相切于点(0,3),圆心在经过点(2,1)与点(﹣2,﹣3)的直线
轴相切于点(0,3),圆心在经过点(2,1)与点(﹣2,﹣3)的直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)圆![]() 与圆
与圆![]() :
:![]() 相交于M、N两点,求两圆的公共弦MN的长.
相交于M、N两点,求两圆的公共弦MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《数书九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”若把以上这段文字写成公式,即![]() .已知
.已知![]() 满足
满足![]()
![]() .且
.且![]() ,则用以上给出的公式可求得
,则用以上给出的公式可求得![]() 的面积为____.
的面积为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
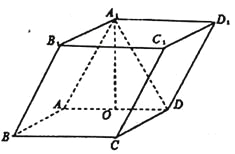
【题目】如图,四棱柱![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
, ![]() ,
, ![]() ,若
,若![]() 为
为![]() 的中点,且
的中点,且![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com