练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f（n）=cos数学公式（n∈N*），则f（1）+f（2）+f（3）+…+f（100）=________．

    解：当n-1时，f（1）=cos=，当n=2时，f（2）=cos，当n=3时，，当n=4时，，
    当n=5时，f（5）=，当n=6时，f（6）=，当n=7时，f（7）=，
    当n=8时，f（8）=，当n=9时，f（9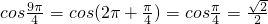）=，…由以上数值出现的规律可以知道，此函数的一个周期为T=8，
    利用函数的周期性，而f（1）+f（2）+f（3）+…f（8）=0，则f（1）+f（2）+f（3）+…+f（100）=f（1）+F（2）+f（3）+f（4）==-1．
    故答案为：-1．
    分析：由已知f（n）=cos（n∈N*）的解析式可以知道该函数是周期函数，所以可以先取一些函数值找起规律即可．
    点评：此题考查了求函数解析式求函数值，并利用观察法得到函数的周期，利用函数的周期性进行对于很多项函数值的求解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f（x）=
    m
    •
    n
    ，其中
    m
    =(sinωx+cosωx，
    		3
    cosωx)    ，
    n
    =（cosωx-sinωx，2sinωx）（ω＞0）．若f（x）图象中相邻的对称轴间的距离不小于
    π
    2
    ．
    （1）求ω的取值范围
    （2）在△ABC中，a，b，c分别为角A，B，C的对边．且a=
    		3
    ，b+c=3，f（A）=1，当ω最大时．求△ABC面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    m
    =(1，cosωx)，
    n
    =(sinωx，
    		3
    )    （ω＞0），函数f(x)=
    m
    •
    n
    ，且f（x）图象上一个最高点的坐标为(
    π
    12
    ，2)    ，与之相邻的一个最低点的坐标为(
    7π
    12
    ，-2)    ．
    （1）求f（x）的解析式；
    （2）在△ABC中，a，b，c是角A、B、C所对的边，且满足a2+c2-b2=ac，求角B的大小以及f（A）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    m
    =(cosx，-sinx)，
    n
    =(cosx，sinx-2
    		3
    cosx)，x∈R    ，令f（x）=
    m
    •
    n
    ．
    （1）当x∈(0，
    π
    2
    )    时，求f（x）的值域；
    （2）已知f(
    α
    2
    )=
    2
    3
    ，求cos(2α-
    2
    3
    π)    的值．

    查看答案和解析>>

    科目：高中数学 来源：2010年重庆市重点高中高考数学模拟试卷9（解析版） 题型：解答题

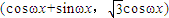    已知m=，n=（cosωx-sinωx，2sinωx），其中ω＞0，若函数f（x）=m•n，且f（x）的对称中心到f（x）对称轴的最近距离不小于
    （Ⅰ）求ω的取值范围；
    （Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，且a=1，b+c=2，当ω取最大值时，f（A）=1，求△ABC的面积．

    查看答案和解析>>

    同步练习册答案