
【题目】如图,在直三棱柱 ![]() 中,
中, ![]() ,A1B与AB1交于点D,A1C与AC1交于点E.求证:
,A1B与AB1交于点D,A1C与AC1交于点E.求证: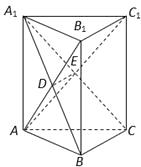
(1)DE∥平面B1BCC1;
(2)平面 ![]()
![]() 平面
平面 ![]() .
.
【答案】
(1)
证明:在直三棱柱 ![]() 中,
中,
四边形A1ACC1为平行四边形.
又E为A1C与AC1的交点,
所以E为A1C的中点,
同理,D为A1B的中点,
所以DE∥BC.
又 ![]() 平面B1BCC1,
平面B1BCC1, ![]() 平面B1BCC1,所以DE∥平面B1BCC1
平面B1BCC1,所以DE∥平面B1BCC1
(2)
在直三棱柱 ![]() 中,
中,
![]() 平面ABC,又
平面ABC,又 ![]() 平面ABC,
平面ABC,
∴ ![]() .
.
又 ![]() ,
, ![]() ,
, ![]() 平面
平面 ![]() ,
,
所以 ![]() 平面
平面 ![]() .
.
因为 ![]() 平面
平面 ![]()
所以平面 ![]()
![]() 平面
平面 ![]() .
.
【解析】(1.)在三角形A1BC中,B、C分别为A1B、A1C中点得到DE//BC,由线面平行的关系可得到DE∥平面B1BCC1;(2.)由 ![]() 、
、 ![]() 得到
得到 ![]() 平面
平面 ![]() ,进而可证平面
,进而可证平面 ![]()
![]() 平面
平面 ![]() .
.
【考点精析】利用直线与平面平行的判定和平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】某车间20名工人年龄数据如表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(Ⅰ) 求这20名工人年龄的众数与平均数;
(Ⅱ) 以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(Ⅲ) 从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的两条渐近线分别为l1 , l2 , 经过右焦点F垂直于l1的直线分别交l1 , l2 于 A,B 两点.若|
的两条渐近线分别为l1 , l2 , 经过右焦点F垂直于l1的直线分别交l1 , l2 于 A,B 两点.若| ![]() |,|
|,| ![]() |,|
|,| ![]() |成等差数列,且
|成等差数列,且 ![]() 与
与 ![]() 反向,则该双曲线的离心率为( )
反向,则该双曲线的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)讨论f(x)的单调性;
(2)设a>0,证明:当0<x<a时,f(x+a)<f(a﹣x);
(3)设x1 , x2是f(x)的两个零点,证明:f′( ![]() )>0.
)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(3,﹣1),|
=(3,﹣1),| ![]() |=
|= ![]() ,
, ![]() =﹣5,
=﹣5, ![]() =x
=x ![]() +(1﹣x)
+(1﹣x) ![]() .
.
(Ⅰ)若 ![]() ,求实数x的值;
,求实数x的值;
(Ⅱ)当| ![]() |取最小值时,求
|取最小值时,求 ![]() 与
与 ![]() 的夹角的余弦值.
的夹角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com