
【题目】对于函数![]() 的图象为C,叙述正确是( )
的图象为C,叙述正确是( )
A.图象C关于直线![]() 对称
对称
B.函数![]() 在区间
在区间![]() 内是增函数
内是增函数
C.由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
D.图象C关于点![]() 对称
对称
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像相邻对称轴之间的距离是
的图像相邻对称轴之间的距离是![]() ,若将
,若将![]() 的图像向右移
的图像向右移![]() 个单位,所得函数
个单位,所得函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)若函数![]() 的零点为
的零点为![]() ,求
,求![]() ;
;
(3)若对任意![]() ,
,![]() 有解,求
有解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的矩形![]() 中,
中, ![]() ,点
,点![]() 为
为![]() 边上异于
边上异于![]() ,
, ![]() 两点的动点,且
两点的动点,且![]() ,
, ![]() 为线段
为线段![]() 的中点,现沿
的中点,现沿![]() 将四边形
将四边形![]() 折起,使得
折起,使得![]() 与
与![]() 的夹角为
的夹角为![]() ,连接
,连接![]() ,
, ![]() .
.

(1)探究:在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,说明点
,若存在,说明点![]() 的位置,若不存在,请说明理由;
的位置,若不存在,请说明理由;
(2)求三棱锥![]() 的体积的最大值,并计算此时
的体积的最大值,并计算此时![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
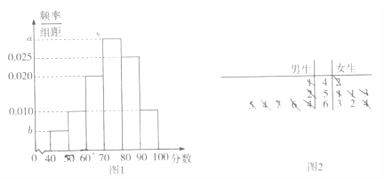
【题目】某教育主管部门到一所中学检查高三年级学生的体质健康情况,从中抽取了![]() 名学生的体质测试成绩,得到的频率分布直方图如图1所示,样本中前三组学生的原始成绩按性别分类所得的茎叶图如图2所示.
名学生的体质测试成绩,得到的频率分布直方图如图1所示,样本中前三组学生的原始成绩按性别分类所得的茎叶图如图2所示.
(Ⅰ)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)估计该校高三学生体质测试成绩的平均数![]() 和中位数
和中位数![]() ;
;
(Ⅲ)若从成绩在![]() 的学生中随机抽取两人重新进行测试,求至少有一名男生的概率.
的学生中随机抽取两人重新进行测试,求至少有一名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标为
的极坐标为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和曲线
和曲线![]() 有三个公共点,求以这三个公共点为顶点的三角形的面积.
有三个公共点,求以这三个公共点为顶点的三角形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2019个数是( )
A. 3972 B. 3974 C. 3991 D. 3993
查看答案和解析>>
科目:高中数学 来源: 题型:
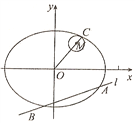
【题目】如图所示,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的中心在原点,点
的中心在原点,点![]() 在椭圆
在椭圆![]() 上,且离心率为
上,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)动直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上一点,直线
上一点,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,
, ![]() 是线段
是线段![]() 上一点,圆
上一点,圆![]() 的半径为
的半径为![]() ,且
,且![]() ,求
,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
B.若三个平面两两相交,其中两个平面的交线与第三个平面平行.则另外两条交线平行;
C.如果![]() 是两条异面直线,那么直线
是两条异面直线,那么直线![]() 一定是异面直线;
一定是异面直线;
D.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 绕
绕![]() 所在直线旋转一周,所形成的几何体的轴截面面积为10.
所在直线旋转一周,所形成的几何体的轴截面面积为10.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com