
【题目】已知函数![]() (
(![]() ,
,![]() ).
).
(1)当![]() (e为自然对数的底数)时,
(e为自然对数的底数)时,
(i)若![]() 在
在![]() 上恰有两个不同的零点,求实数m的取值范围;
上恰有两个不同的零点,求实数m的取值范围;
(ii)若![]() (
(![]() ),求
),求![]() 在
在![]() 上的最大值;
上的最大值;
(2)当![]() 时,
时,![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() .求证:
.求证: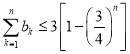 .
.
【答案】(1)(i)![]() .(ii)
.(ii)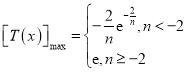 (2)见解析
(2)见解析
【解析】
(1)![]() 时,(i)
时,(i)![]() ,
,![]() ,判断函数的单调性,求解函数的最值,推出m的范围.(ii)
,判断函数的单调性,求解函数的最值,推出m的范围.(ii)![]() (
(![]() ),
),![]() .通过
.通过
①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,利用函数的导数,求解函数的最值.
时,利用函数的导数,求解函数的最值.
(2)![]() 时,
时,![]() ,
,![]() ,转化求解函数的通项公式,利用不等式求解结果即可.
,转化求解函数的通项公式,利用不等式求解结果即可.
(1)![]() 时,(i)
时,(i)![]() ,
,![]() ,
,
故![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增;
上单调递增;
故![]() 在
在![]() 上恰有两个相异实根,
上恰有两个相异实根,
故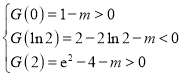 ,解得
,解得![]() .
.
(ii)![]() (
(![]() ),∴
),∴![]() .
.
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,则此时
上为增函数,则此时![]() ;
;
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,
故![]() 在
在![]() 上为增函数,此时
上为增函数,此时![]() ;
;
③当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,
若![]() ,即
,即![]() 时,故
时,故![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,
此时![]() ,
,
若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上为增函数,则此时
上为增函数,则此时![]() ;
;
综上所述: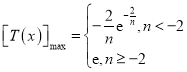 .
.
(2)![]() 时,
时,![]() ,
,![]() ,
,
即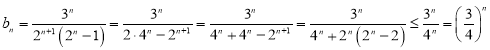 ,
,
所以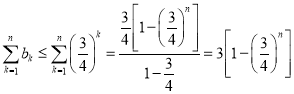 .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:
【题目】已知过点P(4,0)的动直线与抛物线C:![]() 交于点A,B,且
交于点A,B,且![]() (点O为坐标原点).
(点O为坐标原点).
(1)求抛物线C的方程;
(2)当直线AB变动时,x轴上是否存在点Q使得点P到直线AQ,BQ的距离相等,若存在,求出点Q坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆Q经过定点![]() ,且与定直线
,且与定直线![]() 相切(其中a为常数,且
相切(其中a为常数,且![]() ).记动圆圆心Q的轨迹为曲线C.
).记动圆圆心Q的轨迹为曲线C.
(1)求C的方程,并说明C是什么曲线?
(2)设点P的坐标为![]() ,过点P作曲线C的切线,切点为A,若过点P的直线m与曲线C交于M,N两点,则是否存在直线m,使得
,过点P作曲线C的切线,切点为A,若过点P的直线m与曲线C交于M,N两点,则是否存在直线m,使得![]() ?若存在,求出直线m斜率的取值范围;若不存在,请说明理由.
?若存在,求出直线m斜率的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两同学在复习数列时发现原来曾经做过的一道数列问题因纸张被破坏,导致一个条件看不清,具体如下:等比数列![]() 的前n项和为
的前n项和为![]() ,已知_____,
,已知_____,
(1)判断![]() ,
,![]() ,
,![]() 的关系;
的关系;
(2)若![]() ,设
,设![]() ,记
,记![]() 的前n项和为
的前n项和为![]() ,证明:
,证明:![]() .
.
甲同学记得缺少的条件是首项a1的值,乙同学记得缺少的条件是公比q的值,并且他俩都记得第(1)问的答案是![]() ,
,![]() ,
,![]() 成等差数列.如果甲、乙两同学记得的答案是正确的,请你通过推理把条件补充完整并解答此题.
成等差数列.如果甲、乙两同学记得的答案是正确的,请你通过推理把条件补充完整并解答此题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 件次品和
件次品和![]() 件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出
件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出![]() 件次品或者检测出
件次品或者检测出![]() 件正品时检测结束.
件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用![]() 元,设
元,设![]() 表示直到检测出
表示直到检测出![]() 件次品或者检测出
件次品或者检测出![]() 件正品时所需要的检测费用(单位:元),求
件正品时所需要的检测费用(单位:元),求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,四个顶点恰好构成了一个边长为
,四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形.
的菱形.
(1)求椭圆的标准方程;
(2)已知直线![]() ,
,![]() 过右焦点F2,且它们的斜率乘积为
过右焦点F2,且它们的斜率乘积为![]() ,设
,设![]() ,
,![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com