
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
(1)根据以上数据完成下列![]() 的列联表;
的列联表;
(2)能否有99%的把握认为其亲属的饮食习惯与年龄有关,并写出简要分析.
主食蔬菜 | 主食肉类 | 合计 |
| |
50岁以下 | ||||
50岁以上 | ||||
合计 | ||||
参考公式: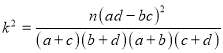
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,直线l过点P(1,1),且倾斜角α=![]() .以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.
.以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.
(1)求圆C的直角坐标方程;
(2)设直线l与圆C交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四色猜想是世界三大数学猜想之一,1976年数学家阿佩尔与哈肯证明,称为四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用![]() ,
,![]() ,
,![]() ,
,![]() 四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为
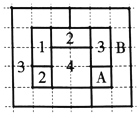
四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为![]() ,粗实线围城的各区域上分别标有数字
,粗实线围城的各区域上分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的四色地图符合四色定理,区域
的四色地图符合四色定理,区域![]() 和区域
和区域![]() 标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为
标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为![]() 的区域的概率所有可能值中,最大的是( )
的区域的概率所有可能值中,最大的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为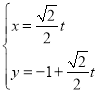 (t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为
(t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设P(0,-1),直线l与C的交点为M,N,线段MN的中点为Q,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为正数的等差数列,数列
是公差为正数的等差数列,数列![]() 为等比数列,且
为等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设数列![]() 是由所有
是由所有![]() 的项,且
的项,且![]() 的项组成的数列,且原项数先后顺序保持不变,求数列
的项组成的数列,且原项数先后顺序保持不变,求数列![]() 的前2019项的和
的前2019项的和![]() ;
;
(3)对任意给定的![]() 是否存在
是否存在![]() 使
使![]() 成等差数列?若存在,用
成等差数列?若存在,用![]() 分别表示
分别表示![]() 和
和![]() (只要写出一组即可);若不存在,请说明理由.
(只要写出一组即可);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;②“
”;②“![]() ”是“
”是“![]() ”的必要不充分条件;③命题“
”的必要不充分条件;③命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;④命题“若
”;④命题“若![]() ,则
,则![]() ”的逆命题为真命题.其中所有正确命题的序号是_________.
”的逆命题为真命题.其中所有正确命题的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,过点
,过点![]() 的直线
的直线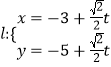 (
(![]() 为参数)与曲线
为参数)与曲线![]() 相交于点
相交于点![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 的平面直角坐标系方程和直线
的平面直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆的方程为(x-1)2+(y-1)2=9,P(2,2)是该圆内一点,过点P的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com