
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合.曲线 ![]() (t为参数),曲线C2的极坐标方程为ρ=ρcos2θ+8cosθ. (Ⅰ)将曲线C1 , C2分别化为普通方程、直角坐标方程,并说明表示什么曲线;
(t为参数),曲线C2的极坐标方程为ρ=ρcos2θ+8cosθ. (Ⅰ)将曲线C1 , C2分别化为普通方程、直角坐标方程,并说明表示什么曲线;
(Ⅱ)设F(1,0),曲线C1与曲线C2相交于不同的两点A,B,求|AF|+|BF|的值.
【答案】解:(Ⅰ)曲线 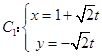 (t为参数),
(t为参数),
将曲线C1的参数方程消去参数t,
化为普通方程得y=﹣x+1,表示一条直线.
曲线C2的极坐标方程为ρ=ρcos2θ+8cosθ.
由cos2θ=1﹣2sin2θ,得曲线C2的方程可变形为ρ2sin2θ=4ρcosθ,
化为直角坐标方程可得y2=4x,曲线C2表示顶点在原点,焦点为(1,0)的抛物线
(Ⅱ)由 ![]() ,消去y,可得x2﹣6x+1=0
,消去y,可得x2﹣6x+1=0
设A(x1,y1),B(x2,y2),则x1+x2=6,
由题意知F(1,0)为曲线C2的焦点
所以|AF|+|BF|=(x1+1)+(x2+1)=x1+x2+2=8
【解析】(Ⅰ)曲线C1的参数方程消去参数t,化为普通方程得y=﹣x+1,表示一条直线;由cos2θ=1﹣2sin2θ,得曲线C2的方程可变形为ρ2sin2θ=4ρcosθ,化为直角坐标方程可得y2=4x,曲线C2表示顶点在原点,焦点为(1,0)的抛物线.(Ⅱ)由 ![]() ,得x2﹣6x+1=0,由题意知F(1,0)为曲线C2的焦点,由此能求出|AF|+|BF|的值.
,得x2﹣6x+1=0,由题意知F(1,0)为曲线C2的焦点,由此能求出|AF|+|BF|的值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数h(x)=(m2﹣5m+1)xm+1为幂函数,且为奇函数.
(1)求m的值;
(2)求函数g(x)=h(x)+ ![]() 在x∈[0,
在x∈[0, ![]() ]的值域.
]的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根据上表可得回归直线方程 ![]() ,其中
,其中 ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,据此估计,该社区一户居民年收入为15万元家庭的年支出为万元.
,据此估计,该社区一户居民年收入为15万元家庭的年支出为万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》规定,公民全月工资、薪金(扣除三险一金后)所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额个人所得税计算公式:应纳税额=工资-三险一金=起征点. 其中,三险一金标准是养老保险8%、医疗保险2%、失业保险1%、住房公积金8%,此项税款按下表分段累计计算:
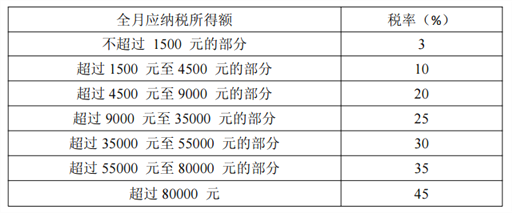
(1)某人月收入15000元(未扣三险一金),他应交个人所得税多少元?
(2)某人一月份已交此项税款为1094元,那么他当月的工资(未扣三险一金)所得是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读与探究
人教A版《普通高中课程标准实验教科书 数学4(必修)》在第一章的小结中写到:
将角放在直角坐标系中讨论不但使角的表示有了统一的方法,而且使我们能够借助直角坐标系中的单位圆,建立角的变化与单位圆上点的变化之间的对应关系,从而用单位圆上点的纵坐标、横坐标来表示圆心角的正弦函数、余弦函数.因此,正弦函数、余弦函数的基本性质与圆的几何性质(主要是对称性)之间存在着非常紧密的联系.例如,和单位圆相关的“勾股定理”与同角三角函数的基本关系有内在的一致性;单位圆周长为![]() 与正弦函数、余弦函数的周期为
与正弦函数、余弦函数的周期为![]() 是一致的;圆的各种对称性与三角函数的奇偶性、诱导公式等也是一致的等等.因此,三角函数的研究过程能够很好地体现数形结合思想.
是一致的;圆的各种对称性与三角函数的奇偶性、诱导公式等也是一致的等等.因此,三角函数的研究过程能够很好地体现数形结合思想.

依据上述材料,利用正切线可以讨论研究得出正切函数![]() 的性质.
的性质.
比如:由图1.2-7可知,角![]() 的终边落在四个象限时均存在正切线;角
的终边落在四个象限时均存在正切线;角![]() 的终边落在
的终边落在![]() 轴上时,其正切线缩为一个点,值为
轴上时,其正切线缩为一个点,值为![]() ;角
;角![]() 的终边落在
的终边落在![]() 轴上时,其正切线不存在;所以正切函数
轴上时,其正切线不存在;所以正切函数![]() 的定义域是
的定义域是![]() .
.
(1)请利用单位圆中的正切线研究得出正切函数![]() 的单调性和奇偶性;
的单调性和奇偶性;
(2)根据阅读材料中途1.2-7,若角![]() 为锐角,求证:
为锐角,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,E、F分别是棱DD1、C1D1的中点. 
(Ⅰ)证明:平面ADC1B1⊥平面A1BE;
(Ⅱ)证明:B1F∥平面A1BE;
(Ⅲ)若正方体棱长为1,求四面体A1﹣B1BE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com