
°æƒø°øƒ≥÷÷…Ã∆∑µƒ –≥°–Ë«Û¡ø![]() £®ÕÚº˛£©°¢ –≥°π©”¶¡ø
£®ÕÚº˛£©°¢ –≥°π©”¶¡ø![]() £®ÕÚº˛£©”Î –≥°º€∏Ò
£®ÕÚº˛£©”Î –≥°º€∏Ò![]() £®‘™/º˛£©∑÷±Ω¸À∆µÿ¬˙◊„œ¬¡–πÿœµ£∫
£®‘™/º˛£©∑÷±Ω¸À∆µÿ¬˙◊„œ¬¡–πÿœµ£∫ ![]() £¨
£¨ ![]() £Æµ±
£Æµ±![]() ±µƒ –≥°º€∏Ò≥∆Œ™ –≥°∆Ω∫‚º€∏Ò£¨¥À ±µƒ–Ë«Û¡ø≥∆Œ™∆Ω∫‚–Ë«Û¡ø£Æ
±µƒ –≥°º€∏Ò≥∆Œ™ –≥°∆Ω∫‚º€∏Ò£¨¥À ±µƒ–Ë«Û¡ø≥∆Œ™∆Ω∫‚–Ë«Û¡ø£Æ
£®1£©«Û∆Ω∫‚º€∏Ò∫Õ∆Ω∫‚–Ë«Û¡ø£ª
£®2£©»Ù∏√…Ã∆∑µƒ –≥°œ˙ €¡ø![]() £®ÕÚº˛£© « –≥°–Ë«Û¡ø
£®ÕÚº˛£© « –≥°–Ë«Û¡ø![]() ∫Õ –≥°π©”¶¡ø
∫Õ –≥°π©”¶¡ø![]() ¡Ω’þ÷–µƒΩœ–°’þ£¨∏√…Ã∆∑µƒ –≥°œ˙ €∂Ó
¡Ω’þ÷–µƒΩœ–°’þ£¨∏√…Ã∆∑µƒ –≥°œ˙ €∂Ó![]() £®ÕÚ‘™£©µ»”⁄ –≥°œ˙ €¡ø
£®ÕÚ‘™£©µ»”⁄ –≥°œ˙ €¡ø![]() ”Î –≥°º€∏Ò
”Î –≥°º€∏Ò![]() µƒ≥Àª˝£Æ
µƒ≥Àª˝£Æ
¢Ÿµ± –≥°º€∏Ò![]() »°∫Œ÷µ ±£¨ –≥°œ˙ €∂Ó
»°∫Œ÷µ ±£¨ –≥°œ˙ €∂Ó![]() »°µ√◊Ó¥Û÷µ£ª
»°µ√◊Ó¥Û÷µ£ª
¢⁄µ± –≥°œ˙ €∂Ó![]() »°µ√◊Ó¥Û÷µ ±£¨Œ™¡À πµ√¥À ±µƒ –≥°º€∏Ò«°∫√ «–¬µƒ –≥°∆Ω∫‚º€∏Ò£¨‘Ú’˛∏Æ”¶∏√∂‘√øº˛…Ã∆∑’˜À∞∂ý…Ÿ‘™£ø
»°µ√◊Ó¥Û÷µ ±£¨Œ™¡À πµ√¥À ±µƒ –≥°º€∏Ò«°∫√ «–¬µƒ –≥°∆Ω∫‚º€∏Ò£¨‘Ú’˛∏Æ”¶∏√∂‘√øº˛…Ã∆∑’˜À∞∂ý…Ÿ‘™£ø
°æ¥∞∏°ø£®1£©∆Ω∫‚º€∏Ò «30‘™£¨∆Ω∫‚–Ë«Û¡ø «40ÕÚº˛£Æ£®2£©¢Ÿ –≥°º€∏Ò «35‘™ ±£¨ –≥°◊Ðœ˙ €∂Ó![]() »°µ√◊Ó¥Û÷µ£Æ¢⁄’˛∏Æ”¶∏√∂‘√øº˛…Ã∆∑’˜7.5‘™£Æ
»°µ√◊Ó¥Û÷µ£Æ¢⁄’˛∏Æ”¶∏√∂‘√øº˛…Ã∆∑’˜7.5‘™£Æ
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©¡Ó![]() £¨µ√
£¨µ√![]() £¨ø…µ√
£¨ø…µ√![]() £¨¥À ±
£¨¥À ±![]() £¨¥”∂¯ø…µ√Ω·π˚£ª£®2£©¢Ÿœ»«Û≥ˆ
£¨¥”∂¯ø…µ√Ω·π˚£ª£®2£©¢Ÿœ»«Û≥ˆ![]() £¨¥”∂¯µ√
£¨¥”∂¯µ√![]() £¨∏˘æð∂˛¥Œ∫Ø ˝µƒ–‘÷ ∑÷±«Û≥ˆ¡Ω∂Œ∫Ø ˝µƒ◊Ó÷µ‘Ÿ±»Ωœ¥Û–°º¥ø…µƒΩ·π˚£ª¢⁄’˛∏Æ”¶∏√∂‘√øº˛…Ã∆∑’˜À∞
£¨∏˘æð∂˛¥Œ∫Ø ˝µƒ–‘÷ ∑÷±«Û≥ˆ¡Ω∂Œ∫Ø ˝µƒ◊Ó÷µ‘Ÿ±»Ωœ¥Û–°º¥ø…µƒΩ·π˚£ª¢⁄’˛∏Æ”¶∏√∂‘√øº˛…Ã∆∑’˜À∞![]() ‘™£¨‘Ú𩔶…õƒ µº º€∏Ò «√øº˛
‘™£¨‘Ú𩔶…õƒ µº º€∏Ò «√øº˛![]() ‘™£¨∏˘æð
‘™£¨∏˘æð![]() ø…µ√Ω·π˚.
ø…µ√Ω·π˚.
‘Ã‚Ω‚Œˆ£∫£®1£©¡Ó![]() £¨µ√
£¨µ√![]() £¨
£¨
π ![]() £¨¥À ±
£¨¥À ±![]() £Æ
£Æ
¥£∫∆Ω∫‚º€∏Ò «30‘™£¨∆Ω∫‚–Ë«Û¡ø «40ÕÚº˛£Æ
£®2£©¢Ÿ”…![]() £¨
£¨ ![]() £¨µ√
£¨µ√![]() £¨
£¨
”…“‚ø…÷™£∫ ![]()
π ![]()
µ±![]() ±£¨
±£¨ ![]() £¨º¥
£¨º¥![]() ±£¨
±£¨ ![]() £ª
£ª
µ±![]() ±£¨
±£¨ ![]() £¨º¥
£¨º¥![]() ±£¨
±£¨ ![]() £¨
£¨
◊€ ˆ£∫µ±![]() ±£¨
±£¨ ![]() ±£¨
±£¨ ![]() £Æ
£Æ
¥£∫ –≥°º€∏Ò «35‘™ ±£¨ –≥°◊Ðœ˙ €∂Ó![]() »°µ√◊Ó¥Û÷µ£Æ
»°µ√◊Ó¥Û÷µ£Æ
¢⁄…Ë’˛∏Æ”¶∏√∂‘√øº˛…Ã∆∑’˜À∞![]() ‘™£¨‘Ú𩔶…õƒ µº º€∏Ò «√øº˛
‘™£¨‘Ú𩔶…õƒ µº º€∏Ò «√øº˛![]() ‘™£¨
‘™£¨
π ![]() £¨
£¨
¡Ó![]() £¨µ√
£¨µ√![]() £¨
£¨
”…“‚ø…÷™…œ ˆ∑Ω≥õƒΩ‚ «![]() £¨¥˙»Î…œ ˆ∑Ω≥õ√
£¨¥˙»Î…œ ˆ∑Ω≥õ√![]() £Æ
£Æ
¥£∫’˛∏Æ”¶∏√∂‘√øº˛…Ã∆∑’˜7.5‘™£Æ


 —Ùπ‚øŒÃ√Õ¨≤Ω¡∑œ∞œµ¡–¥∞∏
—Ùπ‚øŒÃ√Õ¨≤Ω¡∑œ∞œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨»˝¿‚÷˘A1B1C1©ÅABCµƒ≤ý¿‚AA1°Õµ◊√ÊABC£¨AB°ÕAC£¨AB=AA1 £¨ D «¿‚CC1µƒ÷–µ„£Æ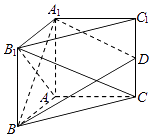
£®¢Ò£©÷§√˜£∫∆Ω√ÊAB1C°Õ∆Ω√ÊA1BD£ª
£®¢Ú£©‘⁄¿‚A1B1…œ «∑ҥʑ⁄“ªµ„E£¨ πC1E°Œ∆Ω√ÊA1BD£ø≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄»˝¿‚÷˘![]() ÷–£¨
÷–£¨ ![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨ ![]() £¨
£¨ ![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ£¨
…œ£¨ ![]() £¨
£¨ ![]() .
.
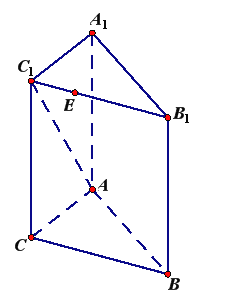
£®1£©«Û÷§£∫ ![]() £ª
£ª
£®2£© ‘ÃΩæø£∫‘⁄![]() …œ «∑ҥʑ⁄µ„
…œ «∑ҥʑ⁄µ„![]() £¨¬˙◊„
£¨¬˙◊„![]() ∆Ω√Ê
∆Ω√Ê![]() £¨»Ù¥Ê‘⁄£¨«Î÷∏≥ˆµ„
£¨»Ù¥Ê‘⁄£¨«Î÷∏≥ˆµ„![]() µƒŒª÷√£¨≤¢∏¯≥ˆ÷§√˜£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”….
µƒŒª÷√£¨≤¢∏¯≥ˆ÷§√˜£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø¥ÛŒ˜—ÛˆŸ”„√øƒÍ∂º“™ƒÊ¡˜∂¯…œ£¨”Œªÿ≤˙µÿ≤˙¬—£¨—–æøˆŸ”„µƒø∆—ߺ“∑¢œ÷ˆŸ”„µƒ”ŒÀŸ![]() £®µ•Œª£∫
£®µ•Œª£∫ ![]() £©”Î∆‰∫ƒ—ı¡øµ•Œª ˝
£©”Î∆‰∫ƒ—ı¡øµ•Œª ˝![]() ÷ƺ‰µƒπÿœµø…“‘±Ì 挙∫Ø ˝
÷ƺ‰µƒπÿœµø…“‘±Ì 挙∫Ø ˝![]() £¨∆‰÷–
£¨∆‰÷–![]() Œ™≥£ ˝£¨“—÷™“ªÃıˆŸ”„‘⁄æ≤÷π ±µƒ∫ƒ—ı¡øŒ™100∏ˆµ•Œª£ª∂¯µ±À¸µƒ”ŒÀŸŒ™
Œ™≥£ ˝£¨“—÷™“ªÃıˆŸ”„‘⁄æ≤÷π ±µƒ∫ƒ—ı¡øŒ™100∏ˆµ•Œª£ª∂¯µ±À¸µƒ”ŒÀŸŒ™![]() ±£¨∆‰∫ƒ—ı¡øŒ™2700∏ˆµ•Œª.
±£¨∆‰∫ƒ—ı¡øŒ™2700∏ˆµ•Œª.
£®1£©«Û≥ˆ”ŒÀŸ![]() ”Î∆‰∫ƒ—ı¡øµ•Œª ˝
”Î∆‰∫ƒ—ı¡øµ•Œª ˝![]() ÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£ª
÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£ª
£®2£©«Ûµ±“ªÃıˆŸ”„µƒ”ŒÀŸ≤ª∏þ”⁄![]() ±£¨∆‰∫ƒ—ı¡ø÷¡∂ý–Ë“™∂ý…Ÿ∏ˆµ•Œª£ø
±£¨∆‰∫ƒ—ı¡ø÷¡∂ý–Ë“™∂ý…Ÿ∏ˆµ•Œª£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™’˝»˝¿‚÷˘![]() £¨
£¨ ![]() «
«![]() µƒ÷–µ„£Æ
µƒ÷–µ„£Æ
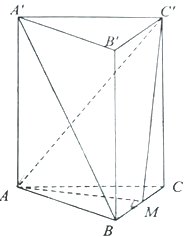
«Û÷§£∫£®1£©![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂®“”ڌ™![]() µƒ∫Ø ˝
µƒ∫Ø ˝![]() «∆Ê∫Ø ˝.
«∆Ê∫Ø ˝.
(1)«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
(2)≈–∂œ∫Ø ˝![]() µƒµ•µ˜–‘≤¢÷§√˜£ª
µƒµ•µ˜–‘≤¢÷§√˜£ª
(2)»Ùπÿ”⁄![]() µƒ≤ªµ» Ω
µƒ≤ªµ» Ω![]() ‘⁄
‘⁄![]() ”–Ω‚£¨«Û µ ˝
”–Ω‚£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄»˝¿‚÷˘ABC©ÅA1B1C1÷–£¨≤ý√ÊABB1A1Œ™æÿ–Œ£¨AB=2£¨AA1=2 ![]() £¨D «AA1µƒ÷–µ„£¨BD”ÎAB1Ωª”⁄µ„O£¨«“CO°Õ∆Ω√ÊABB1A1 £Æ
£¨D «AA1µƒ÷–µ„£¨BD”ÎAB1Ωª”⁄µ„O£¨«“CO°Õ∆Ω√ÊABB1A1 £Æ 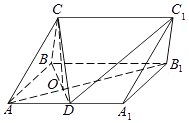
£®1£©÷§√˜£∫CD°ÕAB1£ª
£®2£©»ÙOC=OA£¨«Û÷±œþCD”Î∆Ω√ÊABCÀ˘≥…Ω«µƒ’˝œ“÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨‘⁄¿‚≥§Œ™4µƒ’˝∑ΩÃÂABCD©ÅA1B1C1D1÷–£¨µ„E «¿‚CC1µƒ÷–µ„£¨‘Ú“Ï√Ê÷±œþD1E”ÎACÀ˘≥…Ω«µƒ”ýœ“÷µ « £Æ 
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©= ![]() £®a£æ0£¨«“a°Ÿ1£©‘⁄R…œµ•µ˜µðºı£¨«“πÿ”⁄xµƒ∑Ω≥Ã|f£®x£©|=2©Åx«°∫√”–¡Ω∏ˆ≤ªœýµ»µƒ µ ˝Ω‚£¨‘Úaµƒ»°÷µ∑∂Œß «£® £©
£®a£æ0£¨«“a°Ÿ1£©‘⁄R…œµ•µ˜µðºı£¨«“πÿ”⁄xµƒ∑Ω≥Ã|f£®x£©|=2©Åx«°∫√”–¡Ω∏ˆ≤ªœýµ»µƒ µ ˝Ω‚£¨‘Úaµƒ»°÷µ∑∂Œß «£® £©
A.£®0£¨ ![]() ]
]
B.[ ![]() £¨
£¨ ![]() ]
]
C.[ ![]() £¨
£¨ ![]() ]°»{
]°»{ ![]() }
}
D.[ ![]() £¨
£¨ ![]() £©°»{
£©°»{ ![]() }
}
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com