
【题目】如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1=4,D是A1C1中点.
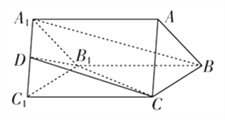
(1)求证:A1B∥平面B1CD;
(2)当三棱锥C-B1C1D体积最大时,求点B到平面B1CD的距离.
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,利用平行四边形性质、三角形中位线定理可得:
,利用平行四边形性质、三角形中位线定理可得: ![]() ,再利用线面平行的判定定理即可证明.(2)设点
,再利用线面平行的判定定理即可证明.(2)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,可得
,可得![]() ,而
,而![]() 故点三棱锥
故点三棱锥![]() 体积最大时,
体积最大时, ![]() ,即
,即![]() 平面
平面![]() ,由(1)知,
,由(1)知, ![]()
可得![]() 到平面
到平面![]() 的距离与
的距离与![]() 到平面
到平面![]() 的距离相等,设
的距离相等,设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]() ,利用体积变换,即可求出.
,利用体积变换,即可求出.
试题解析:
(1)证明:连接BC1交B1C于O,连接DO.在三棱柱ABC-A1B1C1中,四边形BB1C1C为平行四边形,则BO=OC1,又D是A1C1中点,∴DO∥A1B,而DO平面B1CD,A1B平面B1CD,∴A1B∥平面B1CD.
(2)设点C到平面A1B1C1的距离是h,则VC-B1C1D=![]() S△B1C1Dh=
S△B1C1Dh=![]() h,而h≤CC1=4,故当三棱锥C-B1C1D体积最大时,h=CC1=4,即CC1⊥平面A1B1C1.(6分)
h,而h≤CC1=4,故当三棱锥C-B1C1D体积最大时,h=CC1=4,即CC1⊥平面A1B1C1.(6分)
由(1)知BO=OC1,所以B到平面B1CD的距离与C1到平面B1CD的距离相等.
∵CC1⊥平面A1B1C1,B1D平面A1B1C1,
∴CC1⊥B1D.
∵△ABC是等边三角形,D是A1C1中点,
∴A1C1⊥B1D,又CC1∩A1C1=C1,CC1平面AA1C1C,A1C1平面AA1C1C,
∴B1D⊥平面AA1C1C,∴B1D⊥CD,由计算得:B1D=2![]() ,CD=2
,CD=2![]() ,所以S△B1CD=2
,所以S△B1CD=2![]() .
.
设C1到平面B1CD的距离为h′,由VC-B1C1D=VC1-B1CD,得![]() ×4=
×4=![]() S△B1CDh′h′=
S△B1CDh′h′=![]() ,所以B到平面B1CD的距离是
,所以B到平面B1CD的距离是![]() .
.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定, ![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知(x,y)在映射f的作用下的像是(x+y,xy).
(1)求(-2,3)在f作用下的像;
(2)若在f作用下的像是(2,-3),求它的原像.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
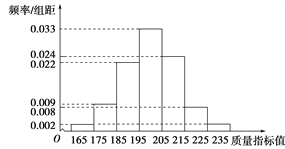
(1)求这500件产品质量指标值的样本平均数![]() 和样本方差s2(同一组中的数据用该组区间的中点值作代表);
和样本方差s2(同一组中的数据用该组区间的中点值作代表);
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2.
,σ2近似为样本方差s2.
(ⅰ)利用该正态分布,求P(187.8<Z<212.2);
(ⅱ)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数.利用(ⅰ)的结果,求E(X).
附: ![]() ≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 为奇函数.
为奇函数.
(1)求b的值;
(2)证明:函数f(x)在区间(1,+∞)上是减函数;
(3)解关于x的不等式f(1+x2)+f(-x2+2x-4)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试求下列函数的定义域与值域:
(1)f(x)=(x-1)2+1,x∈{-1,0,1,2,3};
(2)f(x)=(x-1)2+1;
(3)f(x)=![]() ;
;
(4)f(x)=x-![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com