
(文)已知函数f(x)=![]() x3+
x3+![]() (a-1)x2+bx(a、b为常数)在x=1和x=4处取得极值.
(a-1)x2+bx(a、b为常数)在x=1和x=4处取得极值.
(1)求函数f(x)的解析式;
(2)当x∈[-2,2]时,函数y=f(x)的图象在直线5x+2y-c=0的下方,求实数c的取值范围.
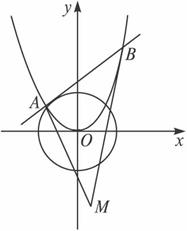
答案:解法一:设抛物线的弦AB与圆x2+y2=1切于点P(x0,y0),则x02+y02=1,过P点的圆的切线方程为x0x+y0y=1.
由 得y0x2+x0x-1=0.(*)
得y0x2+x0x-1=0.(*)
由Δ=x02+4y0=-y02+4y0+1>0,得2![]() <y0<2+
<y0<2+![]() .
.
又∵-1≤y0≤1且y0≠0,∴2![]() <y0≤1且y0≠0.
<y0≤1且y0≠0.
令A(x1,x12),B(x2,x22),知x1、x2是方程(*)的两个实根,由根与系数的关系,得x1+x2=![]() ①,x1x2=
①,x1x2=![]() ②.
②.
过A点的抛物线的切线AM的方程为y-x12=2x1(x-x1),即y=2x1x-x12.③
同理,BM的方程为y=2x2x-x22.④
联立①②③④,解得 ∴x0=
∴x0=
代入x02+y02=1得(![]() )2+(
)2+(![]() )2=1,
)2=1,
整理,得y2-4x2=1(x∈R,y≤-1或y>![]() ),这就是点M的轨迹方程.
),这就是点M的轨迹方程.
解法二:设直线AB的方程为y=kx+b,且A(x1,x12),B(x2,x22),
∵直线AB与圆相切,故![]() =1,即b2=1+k2.
=1,即b2=1+k2.
由 得x2-kx-b=0,
得x2-kx-b=0,
由Δ=k2+4b=b2+4b-1>0,得b<-2![]() 或b>-2+
或b>-2+![]() .
.
又∵b2=1+k2≥1,∴b<-2![]() 或b≥1.由根与系数关系有x1+x2=k,x1x2=-b.
或b≥1.由根与系数关系有x1+x2=k,x1x2=-b.
又过点A的抛物线的切线方程为y-x12=2x1(x-x1),即y=2x1x-x12.①
同理,过点B的抛物线的切线方程为y=2x2x-x22.②
联立①②解得 设M=(x,y),则
设M=(x,y),则
又∵b2=1+k2,∴y2-4x2=1(x∈R,y≤-1或y>2+![]() ),这就是点M的轨迹方程.
),这就是点M的轨迹方程.
(文)解:(1)f′(x)=x2+(a-1)x+b,
由题设得![]() 解之,得
解之,得![]() ∴f(x)=
∴f(x)=![]() x3-
x3-![]() x2+4x.
x2+4x.
(2)由题设知f(x)<-![]() (5x-c),即
(5x-c),即![]() x3-
x3-![]() x2+4x<-
x2+4x<-![]() (5x-c),∴c>
(5x-c),∴c>![]() x3-5x2+13x.
x3-5x2+13x.
设Q(x)=![]() x3-5x2+13x,x∈[-2,2].
x3-5x2+13x,x∈[-2,2].
c只要大于Q(x)的最大值即可.Q′(x)=2x2-10x+13,当x∈[-2,2]时,Q′(x)>0,
∴Q(x)max=Q(2)=![]() .∴c>
.∴c>![]() .
.


科目:高中数学 来源: 题型:
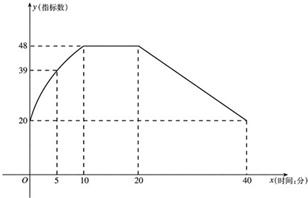 通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.
通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
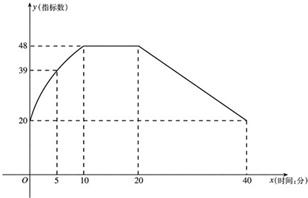 通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.
通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.查看答案和解析>>
科目:高中数学 来源:2010年湖南省澧县一中、岳阳一中高三第三次联考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:湖南省岳澧二校2010届高三第三次联考(理) 题型:解答题
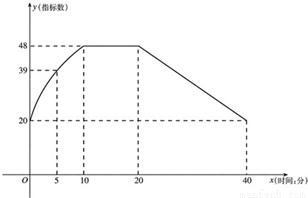
通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散. 学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中). 当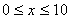 时,图象是抛物线的一部分,当
时,图象是抛物线的一部分,当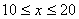 和
和 时,图象是线段.
时,图象是线段.
(1)当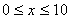 时,求注意力指标数y与时间x的函数关系式;
时,求注意力指标数y与时间x的函数关系式;
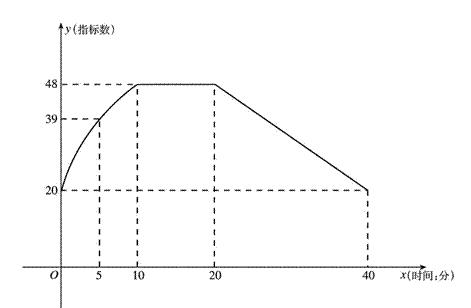 (2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.
(2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com