
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且 ![]() .
. 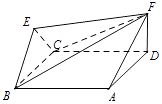
(1)若∠BCD=60°,求证:BC⊥EF;
(2)若∠CBA=60°,求直线AF与平面FBE所成角的正弦值.
【答案】
(1)证明:如图,过点E作EH⊥BC于H,连接HD,∴EH= ![]() .
.
∵平面ABCD⊥平面BCE,EH平面BCE,平面ABCD∩平面BCE=BC,
∴EH⊥平面ABCD.
又∵FD⊥平面ABCD,FD= ![]() ,∴FD∥EH,且FD=EH.
,∴FD∥EH,且FD=EH.
∴四边形EHDF为平行四边形,
∴EF∥HD,
在等边三角形BCD中,BC⊥DH,则BC⊥EF
(2)解:连接HA,由(1),得H为BC中点,又∠CBA=60°,△ABC为等边三角形,
∴HA⊥BC,分别以HB,HA,HE为x,y,z轴建立空间直角坐标系H﹣xyz.
则B(1,0,0),F(﹣2, ![]() ,
, ![]() ),E(0,0,
),E(0,0, ![]() ),A(0,
),A(0, ![]() ,0),
,0),
![]() =(﹣3,
=(﹣3, ![]() ,
, ![]() ),
), ![]() =(﹣1,
=(﹣1, ![]() ,0),
,0), ![]() =(﹣1,0,
=(﹣1,0, ![]() ),
), ![]() =(﹣2,0,
=(﹣2,0, ![]() ),
),
设平面EBF的法向量为 ![]() =(x,y,z),
=(x,y,z),
由 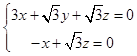 令z=1,
令z=1,
得 ![]() =(
=( ![]() ,2,1),∴直线AF与平面EBF所成角的正弦值为|
,2,1),∴直线AF与平面EBF所成角的正弦值为| ![]() |=
|= ![]() .
.
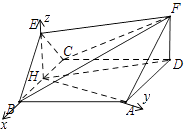
【解析】(1)过点E作EH⊥BC于H,连接HD,证明四边形EHDF为平行四边形,可得EF∥HD,即可证明BC⊥EF;(2)若∠CBA=60°,建立空间直角坐标系,求出平面EBF的法向量,即可求直线AF与平面FBE所成角的正弦值.
【考点精析】关于本题考查的空间中直线与直线之间的位置关系和空间角的异面直线所成的角,需要了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,所成的角为
![]() ,则
,则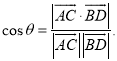 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,A(a,0),B(0,b),O(0,0),△OAB的面积为1.
,A(a,0),B(0,b),O(0,0),△OAB的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N.求证:|AN||BM|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 对任意n∈N* , 点(an , Sn)都在函数 ![]() 的图象上.
的图象上.
(1)求数列{an}的首项a1和通项公式an;
(2)若数列{bn}满足 ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)已知数列{cn}满足 ![]() .若对任意n∈N* , 存在
.若对任意n∈N* , 存在 ![]() ,使得c1+c2+…+cn≤f(x)﹣a成立,求实数a的取值范围.
,使得c1+c2+…+cn≤f(x)﹣a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD﹣A1B1C1D1 , O是底ABCD对角线的交点.求证: 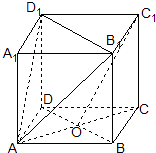
(1)C1O∥面AB1D1;
(2)面BDC1∥面AB1D1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
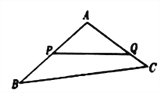
【题目】如图,某生态园将一块三角形地![]() 的一角
的一角![]() 开辟为水果园,已知角
开辟为水果园,已知角![]() 为
为![]() ,
, ![]() 的长度均大于200米,现在边界
的长度均大于200米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 、
、![]() 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块![]() 面积最大?
面积最大?
(2)已知竹篱笆长为![]() 米,
米, ![]() 段围墙高1米,
段围墙高1米, ![]() 段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com