练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

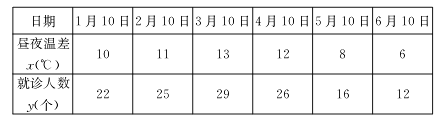
    【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下的资料：

    该兴趣小组确定的研究方案是：现从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选用的2组数据进行检验.

    （1）求选取的2组数据恰好是相邻两个月的概率；

    （2）若选取的是1月与6月的两组数据，请根据2至5月的数据，求出关于的线性回归方程；

    （3）若有线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问（2）中所得线性回归方程是否是理想？

    参考公式：

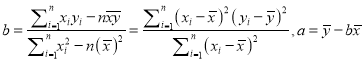
    【答案】（1）；（2）；（3）该小组所得线性回归方程是理想的.

    【解析】试题分析：（1）试验发生包含的事件是从组数据中选取组数据共有种情况，满足条件的事件是抽到相邻两个月的数据的情况有种，根据古典概型的概率公式得到结果；（2）根据所给的数据，求出的平均数，根据公式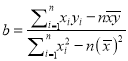求出系数，把和的平均数，代入回归方程求出的值，即可得到线性回归方程.

    试题解析：（1）由题意知本题是一个古典概型，设抽到相邻两个月的数据为事件，试验发生包含的事件是从组数据中选取组数据共有种情况，每种情况都是等可能出现的其中，满足条件的事件是抽到相邻两个月的数据的情况有种， ；（2）由数据求得，由公式求得 ，再由求得 关于线性回归方程为 .

    【方法点晴】本题主要考查古典概型概率公式和线性回归方程求法与应用，属于难题.求回归直线方程的步骤：①依据样本数据画出散点图，确定两个变量具有线性相关关系；②计算的值；③计算回归系数；④写出回归直线方程为； 回归直线过样本点中心是一条重要性质，利用线性回归方程可以估计总体，帮助我们分析两个变量的变化趋势.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】利用随机模拟的方法可以估计图中由曲线与两直线x=2及y=0所围成的阴影部分的面积S：①先产生两组0～1的均匀随机数，a=RAND（　），b=RAND（　）；② 做变换，令x=2a，y=2b；③产生N个点（x，y），并统计落在阴影内的点（x，y）的个数，已知某同学用计算机做模拟试验结果，选取了以下20组数据（如图所示），则据此可估计S的值为____．

    x

    y

    y-0.5*x*x

    0.441414481

    1.849136261

    1.751712889

    1.836710045

    0.508951247

    -1.177800647

    1.389538592

    0.999398689

    0.033989941

    0.745446842

    1.542498362

    1.264652865

    0.981548556

    1.928476536

    1.446757752

    1.87036015

    1.287100762

    -0.462022784

    1.20252176

    1.271691664

    0.548662372

    1.931929493

    0.920911487

    -0.945264297

    0.450507939

    1.561663263

    1.460184562

    1.356178263

    1.856227093

    0.936617353

    0.408489063

    1.564834147

    1.481402489

    0.163980707

    0.135034106

    0.121589269

    1.868152447

    0.350326824

    -1.394669959

    0.252753469

    1.287326597

    1.255384439

    1.253648606

    1.872701968

    1.086884555

    0.679831952

    0.140283887

    -0.090801854

    1.544339084

    0.804655288

    -0.387836316

    1.563089931

    0.872844524

    -0.348780542

    1.17458008

    0.867440167

    0.177620985

    1.057219794

    1.791271879

    1.232415032

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，以原点为圆心，椭圆的短半轴长为半径的与直线相切.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）过定点斜率为的直线与椭圆交于两点，若，求斜率的值；

    （Ⅲ）若（Ⅱ）中的直线与交于两点，设点在上，试探究使的面积为的点共有几个？证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，，，DB平分，为的中点，

    （1）证明： ；

    （2）证明：；

    （3）求直线与平面所成角的正切值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=aln（x2+1）+bx存在两个极值点x1 ， x2 ．
    （1）求证：|x1+x2|＞2；
    （2）若实数λ满足等式f（x1）+f（x2）+a+λb=0，试求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂在政府的帮扶下，准备转型生产一种特殊机器，生产需要投入固定成本万元，生产与销售均已百台计数，且每生产台，还需增加可变成本万元，若市场对该产品的年需求量为台，每生产百台的实际销售收入近似满足函数．

    （）试写出第一年的销售利润（万元）关于年产量（单位：百台，，）的函数关系式：（说明：销售利润=实际销售收入-成本）

    （）因技术等原因，第一年的年生产量不能超过台，若第一年的年支出费用（万元）与年产量（百台）的关系满足，问年产量为多少百台时，工厂所得纯利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了至月份每月号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：

    日期

    1月10日

    2月10日

    3月10日

    4月10日

    5月10日

    6月10日

    昼夜温差

    （）

    就诊人数（个）

    该兴趣小组确定的研究方案是：先从这六组数据中选取组，用剩下的组数据求线性回归方程，再用被选取的组数据进行检验.

    （1）求选取的组数据恰好是相邻两月的概率；

    （2）若选取的是1月与月的两组数据，请根据2至5月份的数据，求出关于的线性回归方程；

    （3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想？

    参考数据，

    （参考公式： ，）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

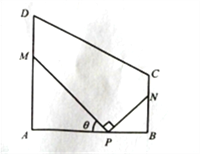
    【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC, 百米， 百米，广场入口P在AB上，且，根据规划，过点P铺设两条相互垂直的笔直小路PM,PN（小路的宽度不计），点M,N分别在边AD,BC上（包含端点），区域拟建为跳舞健身广场， 区域拟建为儿童乐园，其它区域铺设绿化草坪，设.

    （1）求绿化草坪面积的最大值；

    （2）现拟将两条小路PNM,PN进行不同风格的美化，PM小路的美化费用为每百米1万元，PN小路的美化费用为每百米2万元，试确定M,N的位置，使得小路PM,PN的美化总费用最低，并求出最小费用.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，，且对任意，都有：

    ①；②．

    以下三个结论：①；②；③．

    其中正确的个数为（ ）．

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案